Aplicaciones a la espectroscopía infrarroja y Raman
Resumen: Dada una molécula, por ejemplo, [Fe(CO)5] se quiere averiguar cuantas bandas en el IR deben aparecer debidas a las vibraciones C-->O. Se hace un tratamiento de cómo cambian los 5 vectores C-->O por acción de las operaciones. Se obtiene la representación reducible de dimensión 5, se reduce a las representaciones irreducibles y en la Tabla de Caracteres correspondiente al grupo puntual se evalúa cuáles de estas son activas en el IR o en el Raman, cuáles son excluyentes y además si la banda es muy intensa, T o débil A o B.
Algunas consecuencias inmediatas de la simetría
La existencia de algunas propiedades en las moléculas está directamente relacionada con la simetría. A continuación se mencionan dos ejemplos típicos.
a. Actividad óptica
Una molécula quiral es aquella que no puede superponerse con su imagen especular. Las moléculas quirales son ópticamente activas puesto que rotan el plano de la luz polarizada. Una molécula es quiral si no posee ningún eje impropio de rotación Sn, ni las operaciones que son casos especiales de la operación Sn, como son un plano, que es equivalente a la operación S1 y un centro de inversión que es equivalente a la operación S2.
La relación que existe entre los compuestos ópticamente activos es la disimetría, que no es equivalente a asimetría. La asimetría indica carencia de simetría, mientras que la disimetría puede implicar la existencia de algunos elementos de simetría; el término se aplica a moléculas que no poseen ejes impropios de simetría.
b. Polaridad
Una molécula polar es la que tiene un momento dipolar eléctrico permanente. Por consiguiente, cuando existan operaciones de simetría que conviertan un extremo de la molécula en el otro (centro de simetría, plano horizontal) no puede haber polaridad en la molécula, puesto que la carga de un lado se cancela por una carga igual en el otro lado; si están presentes dos o más ejes Cn (n>1), no existe un dipolo porque el vector no puede estar simétricamente a lo largo de más de un eje.
Puede concluirse que los grupos Cn, Cnv y Cs pueden tener momento dipolar eléctrico, y que en el caso de Cn y Cnv éste debe estar a lo largo del eje de rotación. Por otra parte, no puede haber momento dipolar en las moléculas que pertenezcan a los grupos Cnh, Dn, Dnh, Dnd puesto que hay operaciones de simetría que transforman un extremo de la molécula en el otro.
Aplicaciones de la teoría de grupos a la espectroscopía infrarroja y Raman.
Los movimientos vibracionales son aquellos en los que las distancias y ángulos internos de las moléculas cambian periódicamente sin producir una traslación neta del centro de masa de la molécula, ni un momento angular neto. Una molécula de n átomos tiene 3n grados de libertad de movimiento, de los cuales tres corresponden a traslaciones y tres a rotaciones. Entonces, en total, 3n - 6 grados de libertad corresponden a modos normales de vibración.
Como el estudio de las vibraciones en una molécula es el estudio del movimiento de cada átomo, para considerarlo es conveniente colocar un sistema de coordenadas cartesianas en cada uno de ellos, con el átomo en el origen. Cada átomo se mueve en 3 dimensiones, de manera que deben considerarse en total 3n transformaciones, de las cuales 3n - 6 son vibracionales. Los modos normales de vibración se transforman en la forma estipulada por los caracteres de la representación a la cual pertenecen, por lo tanto sólo es necesario determinar los caracteres de las correspondientes matrices de transformación. Esta información se obtiene directamente del conocimiento de la simetría de la molécula, y los vectores de desplazamiento colocados sobre los ejes cartesianos pueden usarse como la base para una representación reducible del grupo de simetría de la molécula.
Por ejemplo, para la molécula de H2O, se tienen en total 9 vectores componentes, tres para cada átomo, de tal manera que una matriz de transformación que represente una operación de simetría será una matriz 9x9.
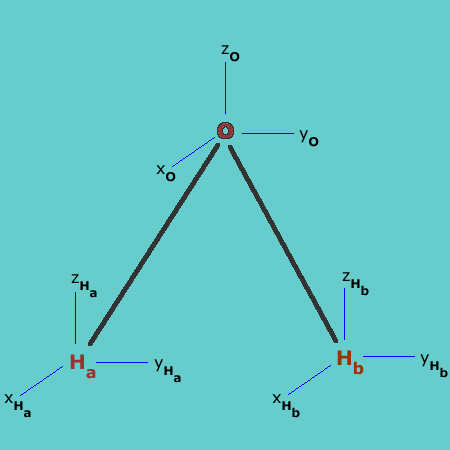
Vectores componentes de la molécula H2O
Para encontrar los elementos de esta matriz, si el átomo cambia de posición por la operación de simetría, se asigna un cero a cada uno de sus tres vectores cartesianos; si el átomo permanece en su posición original y la dirección del vector no cambia, se asigna el número 1 a cada vector y si el átomo permanece en su posición, pero cambia la dirección del vector, se asigna -1. Luego, por suma de los elementos de la diagonal de la matriz se obtiene el carácter de la representación reducible, G.
Entonces, la reflexión σv(xz) para la molécula de H2O se representa como:

Para encontrar el carácter se suman únicamente los elementos diagonales de la matriz, por lo tanto el carácter de la operación σv(xz) para el grupo C2v es 3. Puede realizarse el mismo ejercicio con todas las operaciones de simetría del grupo para encontrar las cuatro matrices de transformación 9x9 correspondientes. Como lo que interesa son sólo los caracteres de las matrices, éstos se pueden hallar rápidamente si se tiene en cuenta que los vectores que contribuyen al carácter de la matriz son únicamente aquellos cuyo origen no se traslada por acción de la operación de simetría. Así, se tiene para las operaciones de simetría de la molécula:
- E: Ningún vector se traslada por la operación identidad, por lo tanto cada uno contribuye con 1 y el carácter de la matriz es 9.
- C2: Los átomos de H cambian de posición, luego sus 6 vectores contribuyen con 0 al carácter. Los vectores x, y del átomo de O se invierten, luego contribuyen con -1 al carácter. El vector z de este átomo permanece igual y contribuye con 1. El carácter es:
- σv(xz): En el ejemplo se ilustró que el carácter es 3.
- σv(yz): Con esta reflexión los H cambian de posición, luego la contribución de sus vectores es 0. El vector x del átomo de O cambia de dirección, por lo tanto su contribución es -1, mientras que los vectores y, z no cambian de dirección, para una contribución individual de 1. El carácter es:
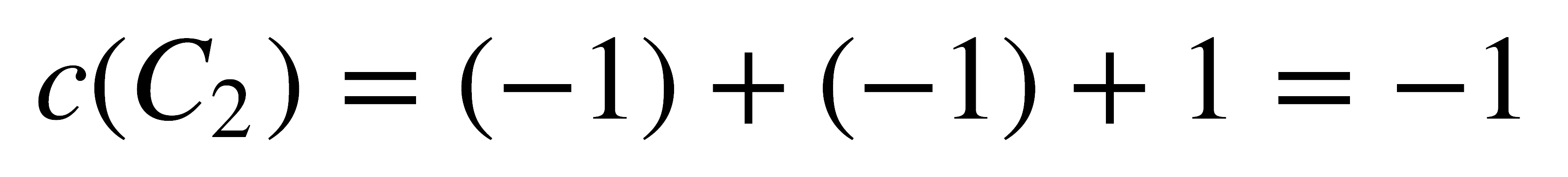
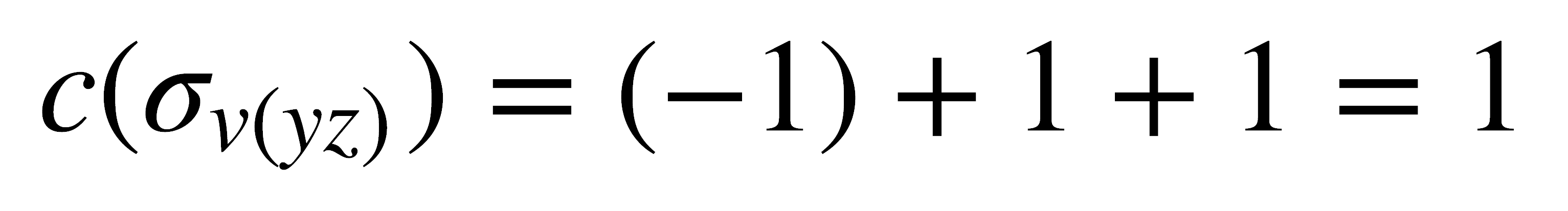
En resumen, el carácter de la representación reducible es:
| C2v | E | C2 | σv(xz) | σv(yz) |
| G | 9 | -1 | 3 | 1 |
El siguiente paso consiste en descomponer G en sus representaciones irreducibles, teniendo en cuenta la Tabla de Caracteres del grupo C2v
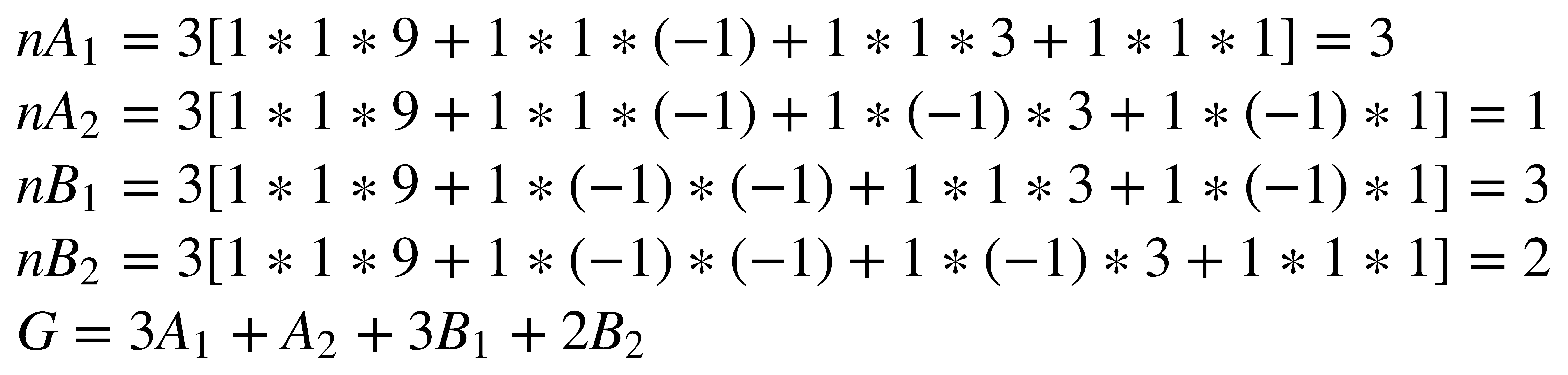
En la representación reducible que da lugar a todas estas representaciones irreducibles se tuvieron en cuenta todos los movimientos posibles de los átomos. Cuando los vectores paralelos están en fase ocurren las traslaciones o rotaciones de la molécula como un todo, que ya se habían mencionado anteriormente, las cuales no deforman a la misma y por lo tanto no constituyen vibraciones propiamente dichas. Entonces hay necesidad de restar las representaciones irreducibles correspondientes a las traslaciones en x, y, z y a las rotaciones sobre x, y, z.
La Tabla de Caracteres del grupo C2v muestra que las traslaciones a lo largo de los ejes x, y, z se transforman como A1 + B1 + B2, y que las rotaciones Rx, Ry, Rz se transforman como A2 + B1 + B2. Al restar estas representaciones de los modos normales de vibración:
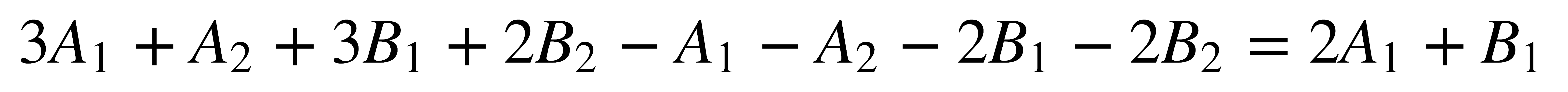
Una vibración molecular es activa en el infrarrojo únicamente si produce un cambio en el momento dipolar de las moléculas. En términos de la teoría de grupos, esto quiere decir que un modo de vibración es activo en el infrarrojo si corresponde a una representación irreducible que se transforme como los ejes de coordenadas cartesianas, puesto que el momento dipolar se transforma como estos ejes. En el caso del agua, los modos de vibración obtenidos (2A1 + B1) tienen la misma simetría de los ejes x, z por lo tanto los dos son activos en el infrarrojo.
En los casos corrientes, y para moléculas con cinco o más átomos, el tratamiento completo anterior es muy tedioso. Como ayuda rápida, el método se utiliza primordialmente para decidir el número de bandas que presentan determinados enlaces de un compuesto, lo cual permitiría distinguir, por ejemplo, entre dos isómeros geométricos.
Como ilustración, en los complejos dioxometálicos del tipo [MO2(LL)2] puede suceder que los grupos oxo se encuentren en posiciones cis- o trans-. La estructura puede asignarse con base en el número de bandas que presenten en el infrarrojo, las cuales se deducen mediante el siguiente tratamiento: En el compuesto [MO2(LL)2] el isómero cis-dioxo pertenece al grupo puntual C2 y el trans- al D2h
Isómeros geométricos del complejo [MO2(LL)2]
cis-dioxo, grupo puntual C2
trans-dioxo, grupo puntual D2h
En este caso, sólo interesa la vibración M=O que se representa por un vector, entonces se seleccionan como base sólo los dos vectores M=O para cada isómero y se determinan los caracteres para cada operación de simetría de cada grupo puntual. Se obtiene para el grupo C2 la representación reducible G1:
| C2 | E | C2 |
| G1 | 2 | 0 |
Para el grupo D2h se obtiene la representación reducible G2:
| D2h | E | C2 | C2'' | C2'' | i | σh | σv' | σv'' |
| G2 | 2 | 2 | 0 | 0 | 0 | 0 | 2 | 2 |
A continuación se descomponen las representaciones reducibles en sus irreducibles. Del carácter reducible de E, 2, en cada caso, se deduce que la representación se puede reducir a dos representaciones irreducibles monodegeneradas A y/o B, o a una doblemente degenerada o bidimensional E, que en este caso, si fuera así, tendría que ser igual a G1 o a G2. Cuando se han seleccionado como base sólo los vectores que representan las vibraciones de los enlaces, no se deben restar las tres rotaciones sobre x, y, z ni las tres traslaciones en las mismas direcciones puesto que no se han considerado todos los movimientos de la molécula.
Como lo que interesa es saber si las representaciones irreducibles que se obtengan son o no activas en el IR, basta sólo con determinar si las representaciones irreducibles que tienen como bases los vectores x, y, o z son propias de la representación reducible en consideración. Para el grupo C2, A tiene componente en z y B, en x, y. Al hacer el ejercicio se encuentra que tanto A como B son representaciones irreducibles de G1 y las dos son activas en el infrarrojo, por lo tanto el isómero cis-[MO2(LL)2] debe presentar dos bandas en el IR en la región típica para enlaces M=O. Para el isómero trans-, las representaciones irreducibles que tienen componentes en x, y, o z son sólo B1u, B2u y B 3u. Al determinar cuáles de ellas forman parte de la representación reducible, se encuentra que sólo B1u hace parte de G2, por lo tanto el isómero trans- únicamente presenta una banda activa en el IR en la región típica para el enlace M=O. Así se pueden diferenciar fácilmente los dos isómeros geométricos.
Las tablas de caracteres también permiten deducir si deben presentarse bandas en Espectroscopía Raman, puesto que sólo son activas aquellas representaciones irreducibles que tengan como base productos vectoriales, xy, xz, yz, x2, x2 - y2, etc. Para ello se procede de manera similar a lo expuesto para el IR. Si se obtiene que una misma representación irreducible propia de la representación reducible es activa tanto en el IR como en el Raman, los espectros correspondientes deben presentar dicha banda a la misma frecuencia tanto en el IR como en el Raman.