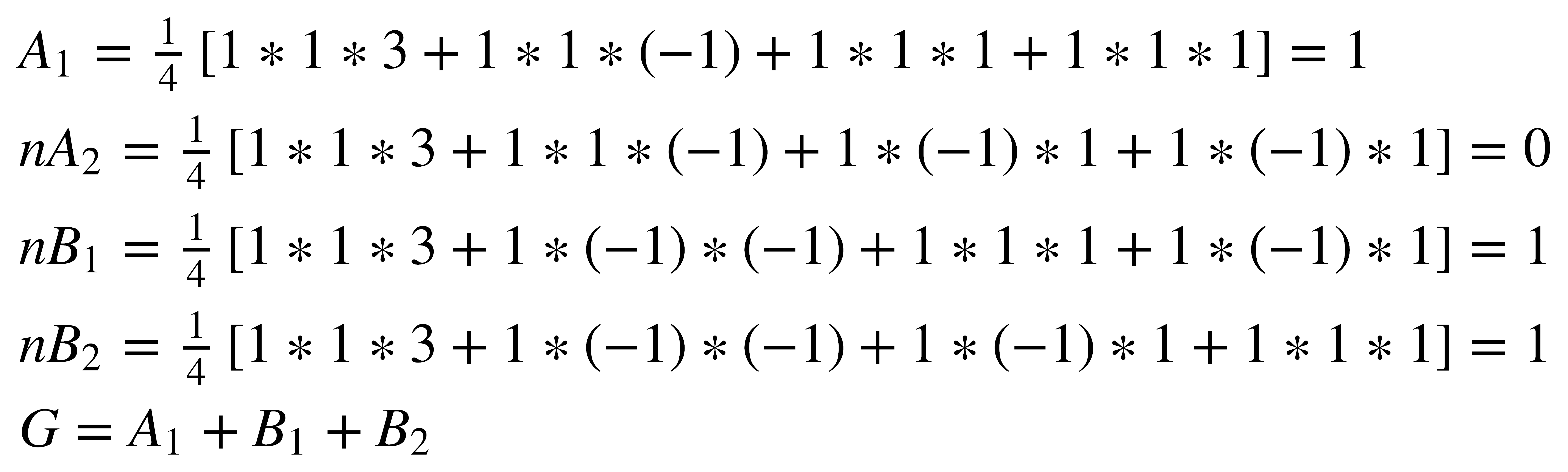Representaciones a través de matrices
Resumen: Una propiedad vectorial o tensorial de una molécula, por ejemplo una vibración o una función orbital, cambia por acción de una operación de simetría, este cambio se representa por un número o por el caracter de una matriz. El conjunto de caracteres generados por el cambio debido a las diferentes operaciones de simetría se llama una representación.
Representaciones de las operaciones de simetría
Cualquier punto de coordenadas (x,y,z) se transforma mediante una operación de simetría en otro punto cuyas nuevas coordenadas son (x',y',z'). Las relaciones de estas nuevas coordenadas con las iniciales dependen de la operación que se lleve a cabo, la cual puede expresarse por medio de una matriz de transformación, tal que:
[matriz de transformación] [x, y, x] = [x', y', z']
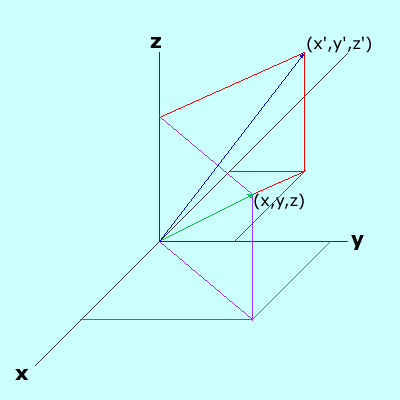
Aplicación de la operación C4 alrededor del eje z
A continuación se explica la construcción de la matriz de transformación para la operación C4 alrededor del eje z. Como se ilustra en la figura anterior, un vector cuyo extremo está definido por las coordenadas (x,y,z) se transforma por la operación C4 en el vector cuyo extremo está definido por (x',y',z'). En término de las coordenadas originales, estas nuevas coordenadas pueden definirse como:
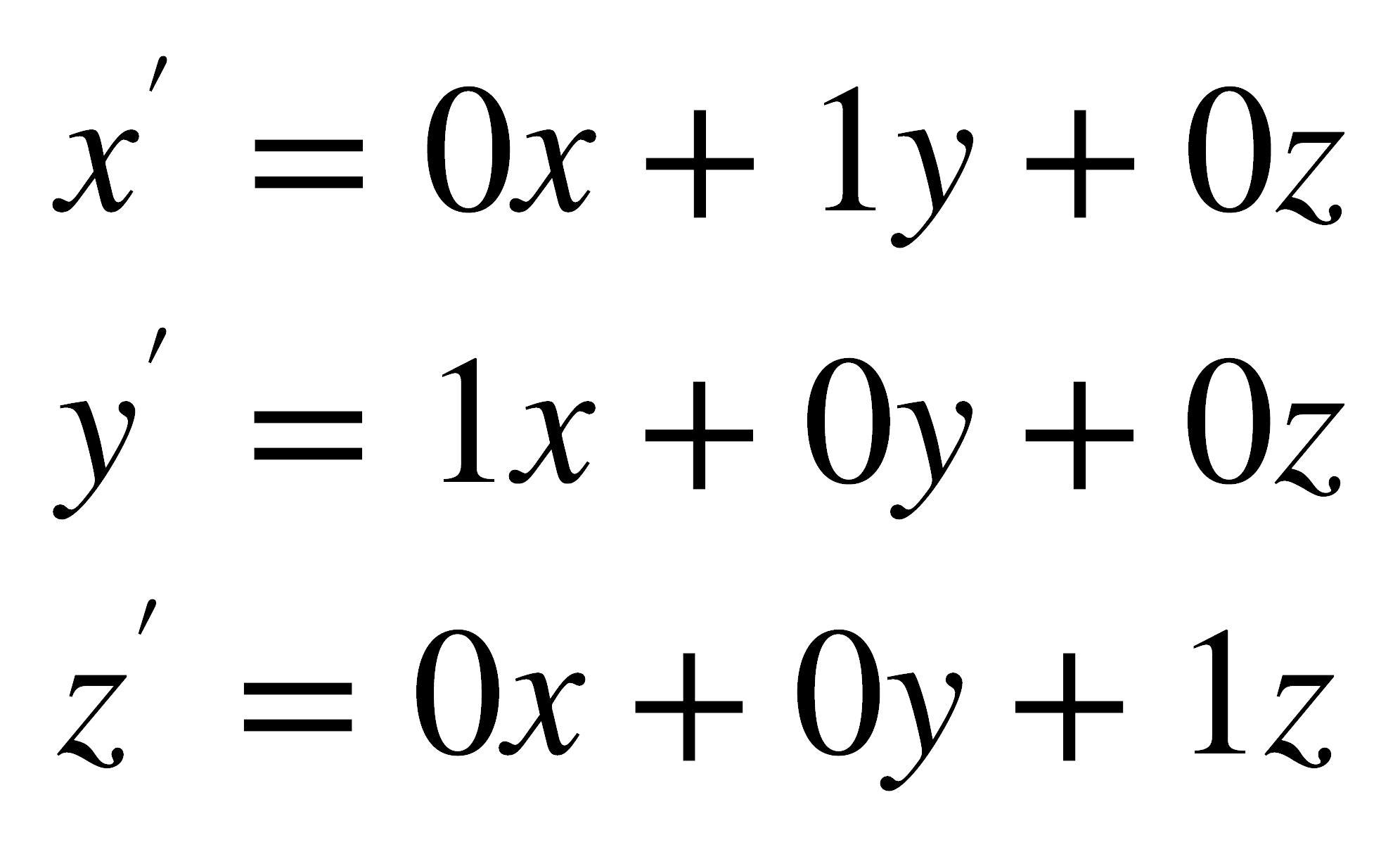
Tomando estos coeficientes en orden se obtiene:
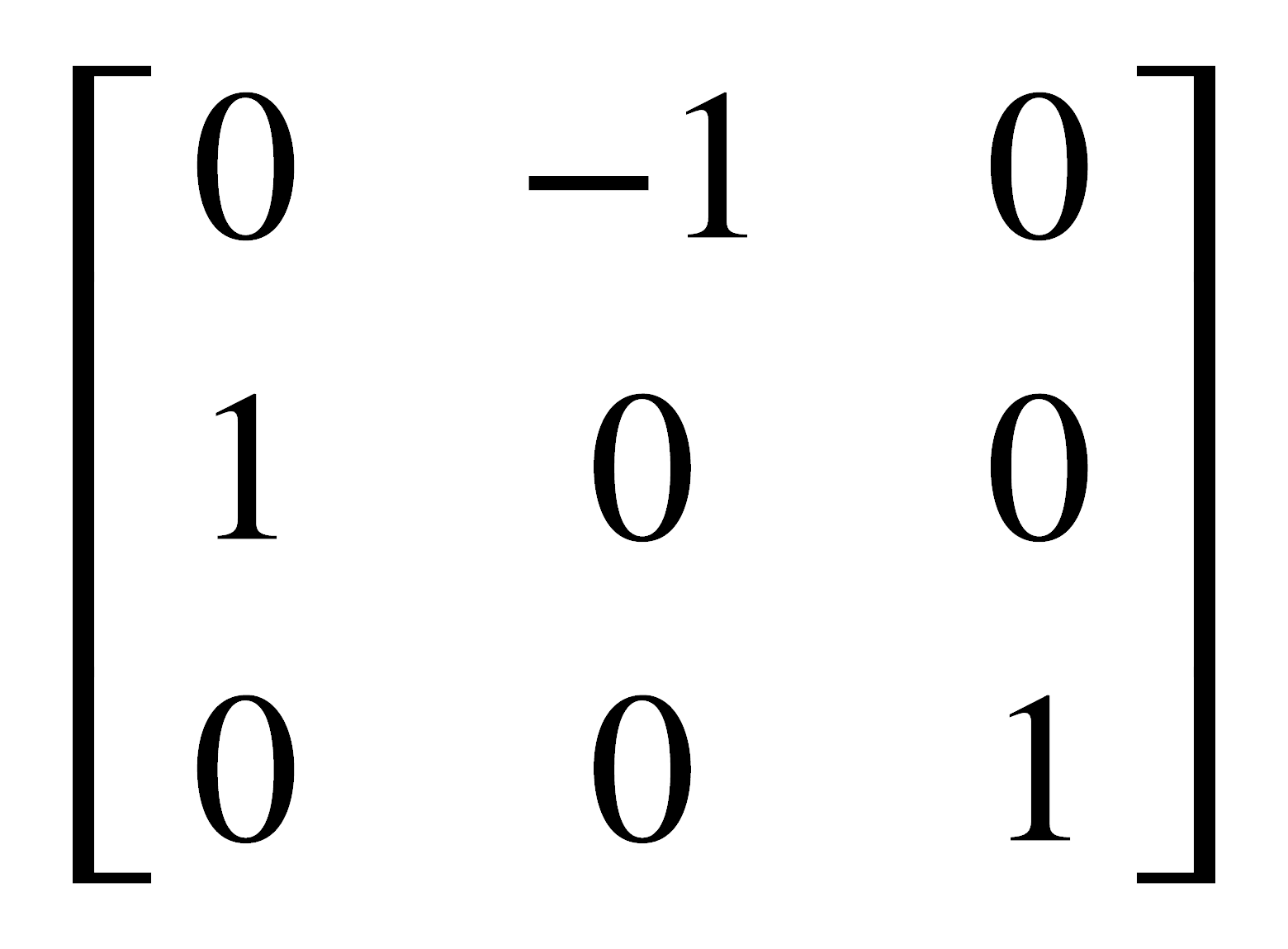
que es una matriz cuadrada de 3x3 y que corresponde a la matriz de transformación que representa la operación C4. Por consiguiente, al hacer actuar esta matriz sobre las coordenadas del punto original (x,y,z) deben obtenerse las del nuevo punto (x',y',z').
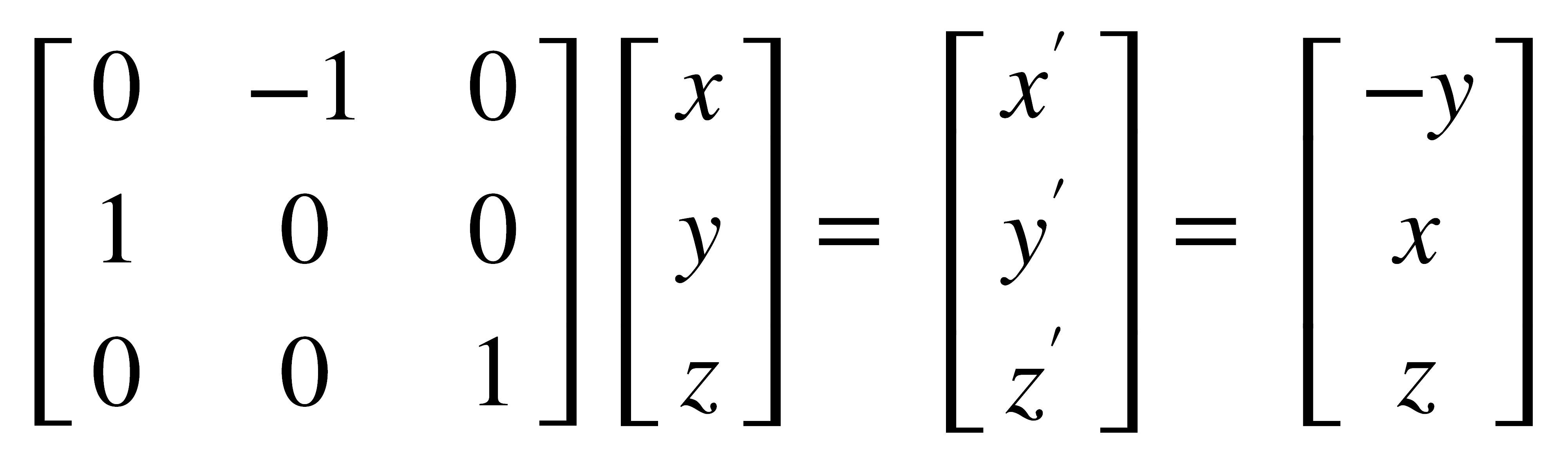
Lo anterior significa que la nueva componente x' es igual al negativo del valor original de y, mientras que la nueva y' es igual al valor original de x; por otra parte, z y z' tienen el mismo valor. Al proceder en la misma forma se encuentran las matrices de transformación que describen las operaciones de simetría más comunes:
Identidad
Cuando un punto de coordenadas (x,y,z) se somete a la operación identidad sus nuevas coordenadas son las mismas iniciales, es decir (x,y,z). En forma matricial, lo anterior se expresa como:

Puede notarse que la operación identidad se describe mediante la matriz unitaria.
Reflexión
Cuando el plano de reflexión coincide con uno de los planos cartesianos (xy, xz, yz), el efecto de la reflexión sobre las coordenadas de un punto es cambiar el signo de la coordenada perpendicular al plano y dejar invariables las coordenadas cuyos ejes definen el plano. Entonces, para las reflexiones sobre los tres planos principales, pueden escribirse las siguientes ecuaciones:
σ(xy)
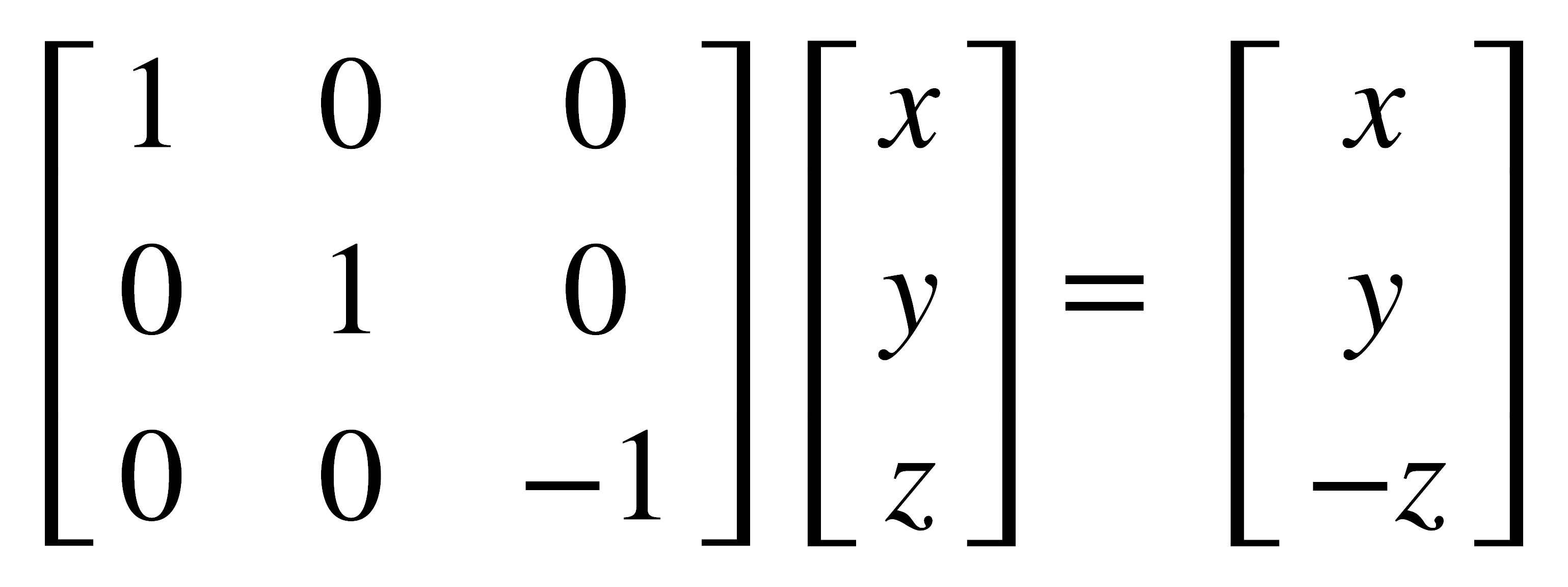
σ(xz)
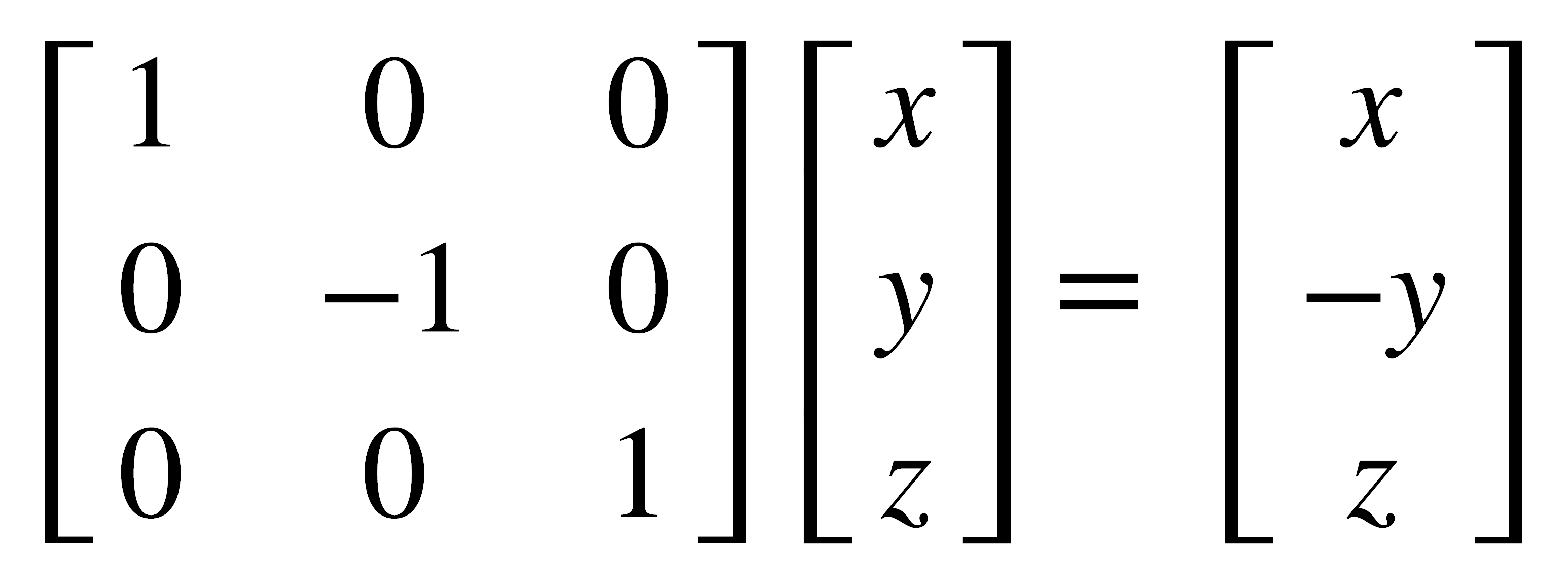
σ(yz)
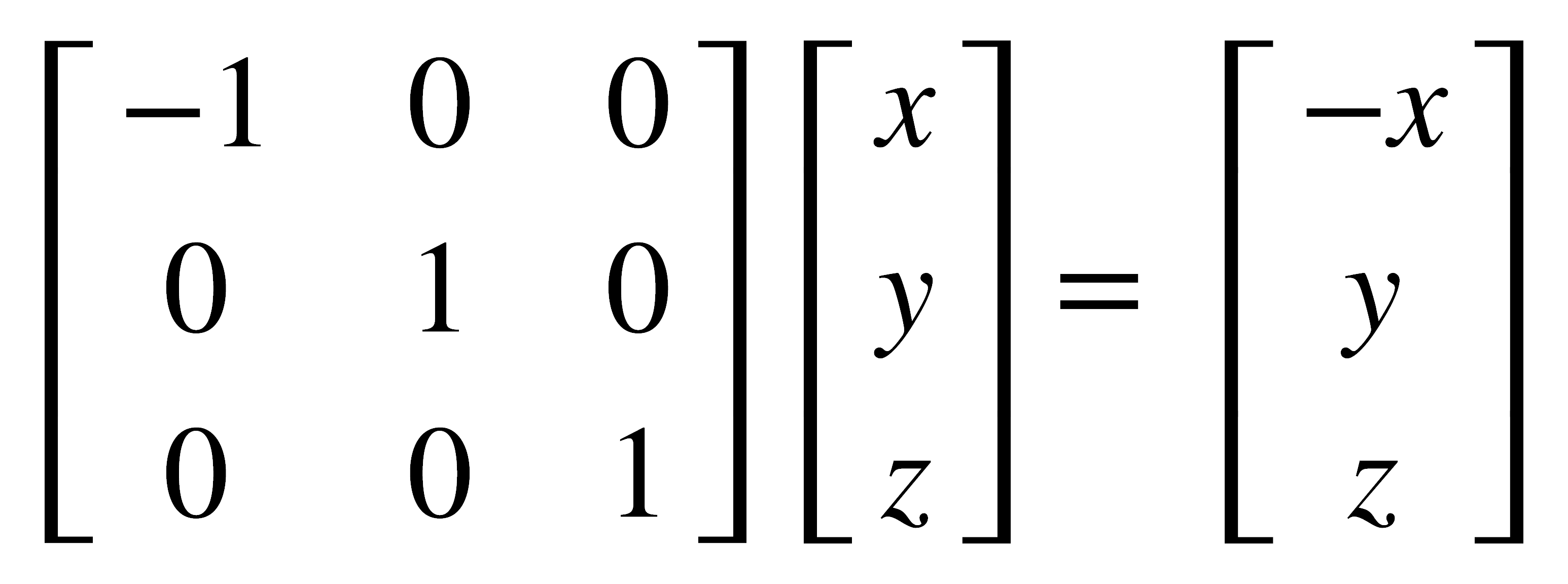
Inversión
La operación inversión cambia los signos de todas las coordenadas del punto inicial, luego puede describirse mediante la ecuación:
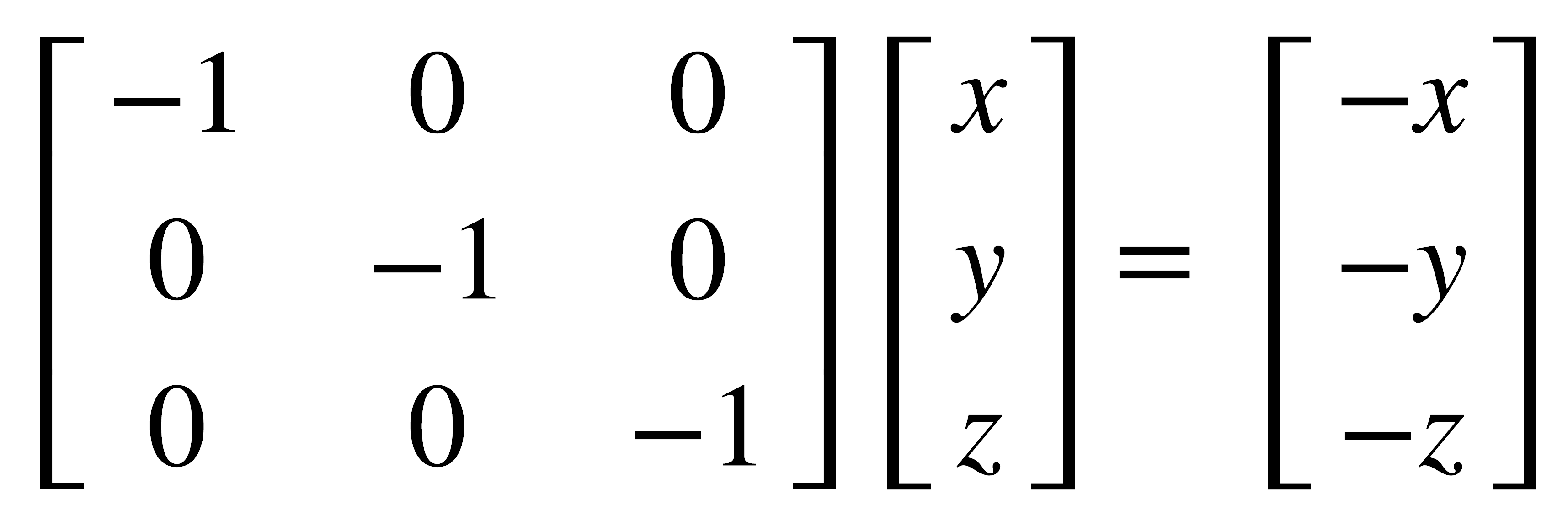
Rotación propia
Como ya se observó para la operación C4, la rotación alrededor de un eje mantiene inalterada la coordenada de este eje. Las otras coordenadas pueden deducirse con ayuda de un diagrama bidimensional. Por ejemplo, si se efectúa la rotación de un vector r̄1 un ángulo θ alrededor del eje z, la coordenada en z permanece como tal; las coordenadas en x,y (x1, y1) cambian a (x2, y2), las cuales definen un nuevo vector r̄2. El problema ahora consiste en encontrar la relación entre las coordenadas iniciales (x1, y1), las coordenadas finales (x2, y2), y el ángulo θ.
En las siguientes dos imágenes se ilustra la transformación de un vector por rotación en un ángulo θ alrededor del eje z. En la imagen de la izquierda se aprecia la representación de los vectores inicial y final, y en la imagen de la derecha la representación bidimensional de los nuevos vectores por rotación de las componentes (x1, y1) del vector inicial.
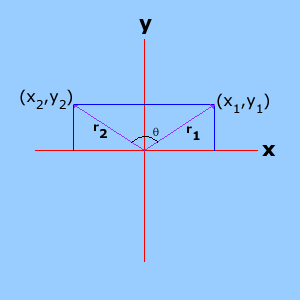
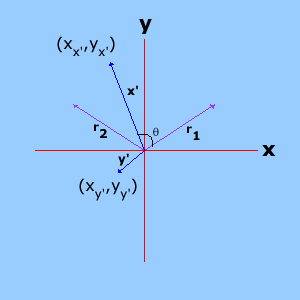
Al rotar un ángulo θ, las componentes x1, y1 se transforman en unos nuevos vectores x̄, ȳ de magnitud x1, y1 respectivamente. Las sumas de las componentes de estos nuevos vectores en x y en y deben ser iguales a x2 y y2. De las imágenes anteriores puede deducirse fácilmente que:
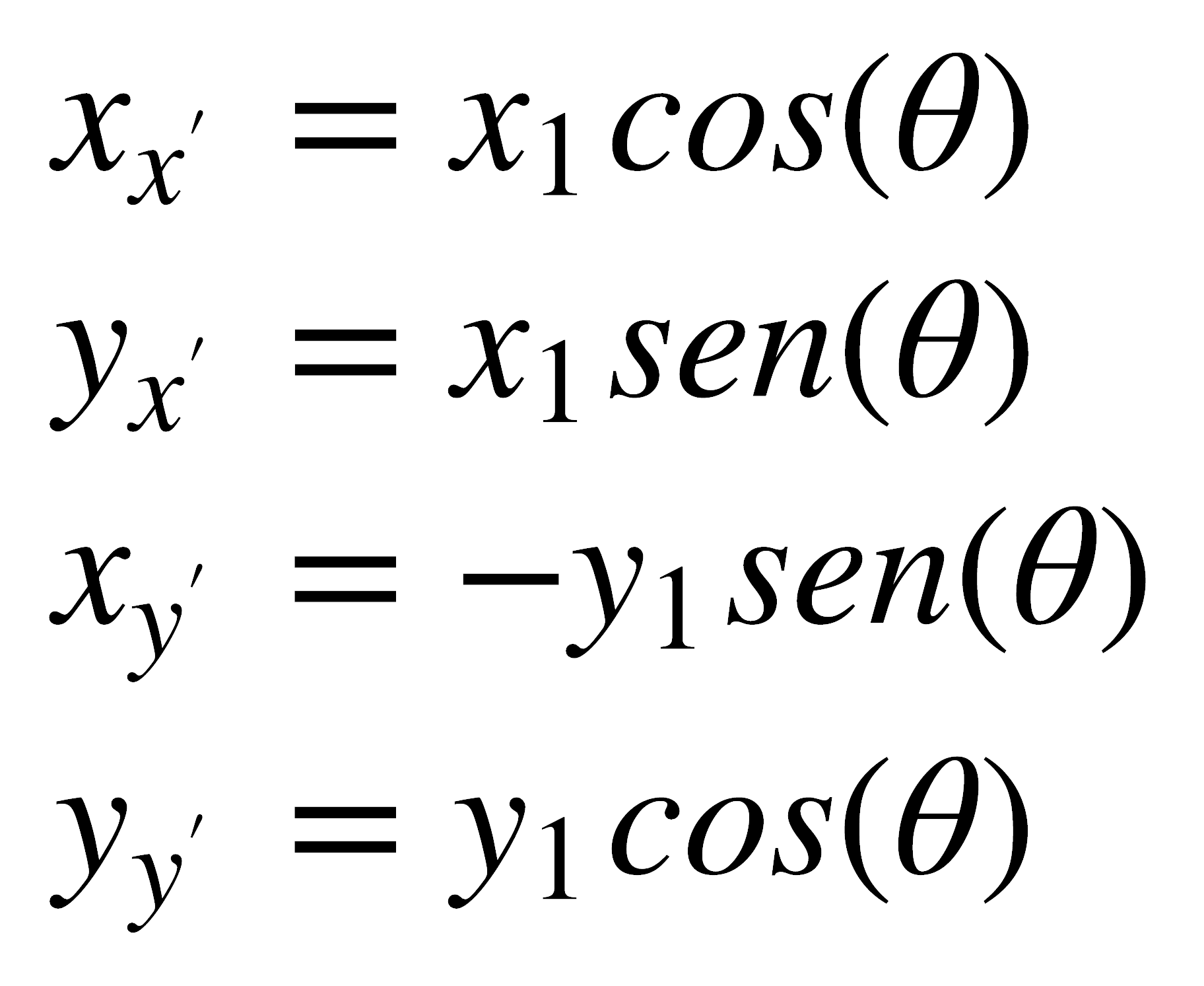
Por lo tanto:
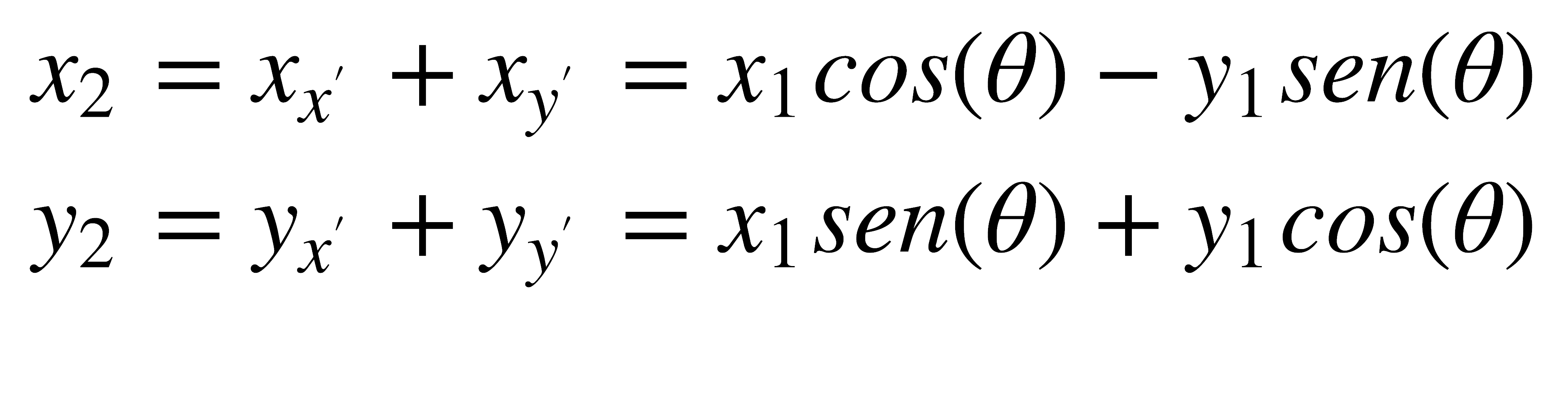
La transformación expresada por las ecuaciones anteriores, en forma matricial, puede escribirse como:
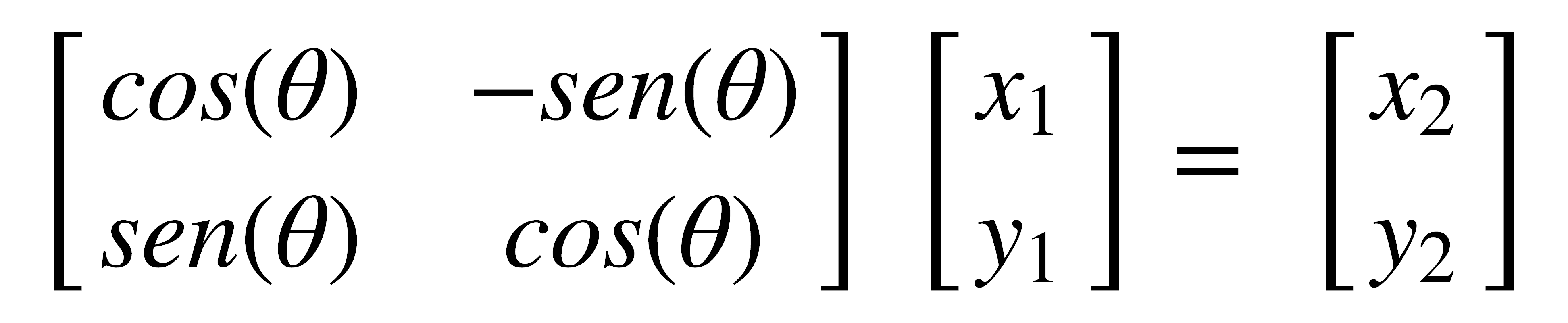
Esta ecuación representa una rotación en sentido inverso a la rotación de las manecillas del reloj, pero si se cambia el sentido de la rotación debe tenerse esto en cuenta al deducir la matriz correspondiente. Al considerarse las tres coordenadas cartesianas, la ecuación matricial que representa una rotación en un ángulo θ alrededor del eje z, en sentido inverso a las manecillas del reloj, es:
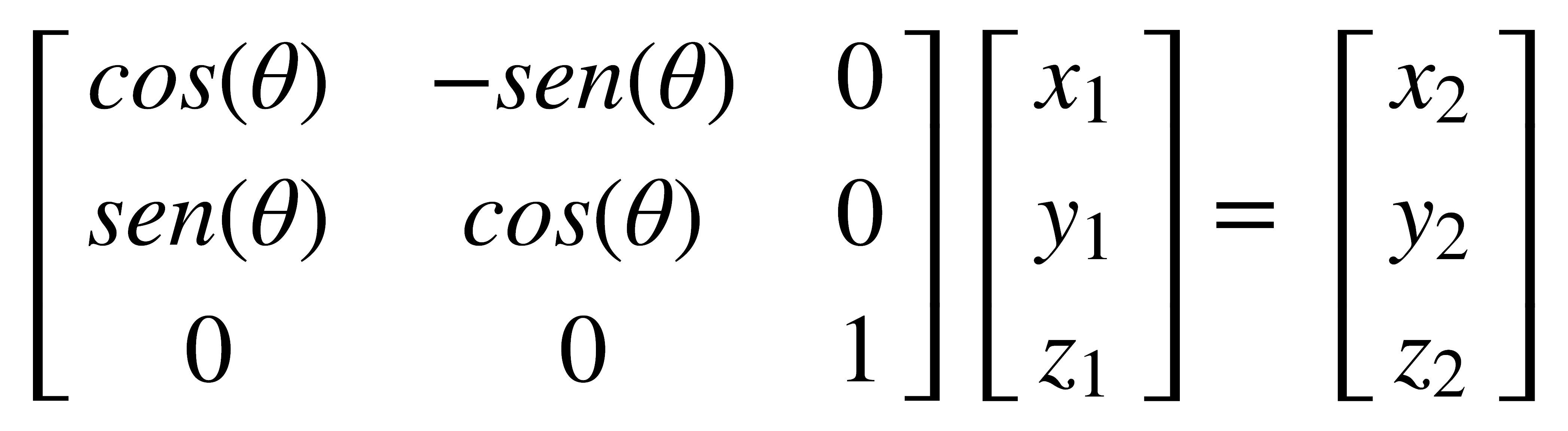
Por ejemplo, para la operación C2 alrededor del eje z, la matriz queda así:
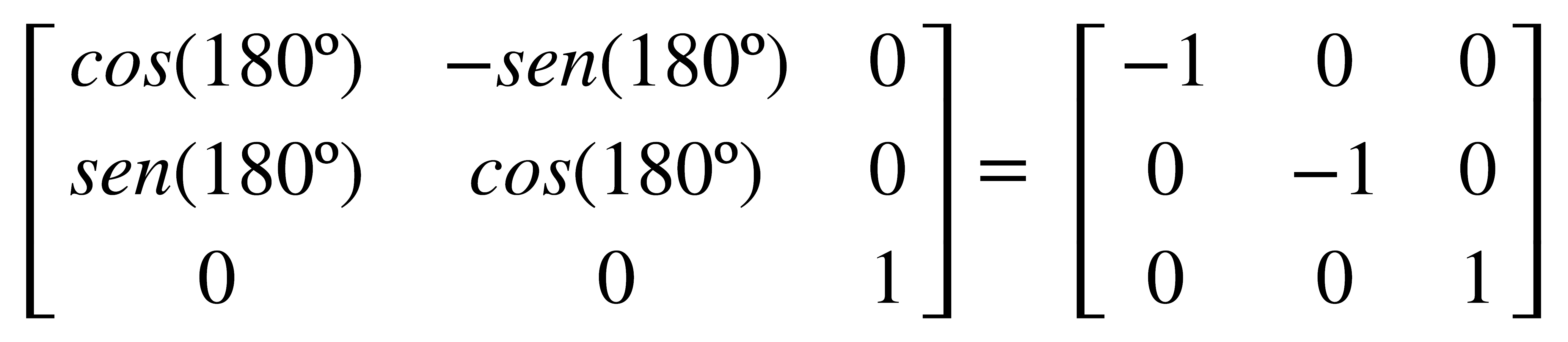
Rotación impropia
Una rotación impropia alrededor del eje z produce la misma transformación que una rotación propia alrededor del mismo eje y adicionalmente cambia el signo de la coordenada en z, luego puede deducirse que la matriz que describe esta operación es:
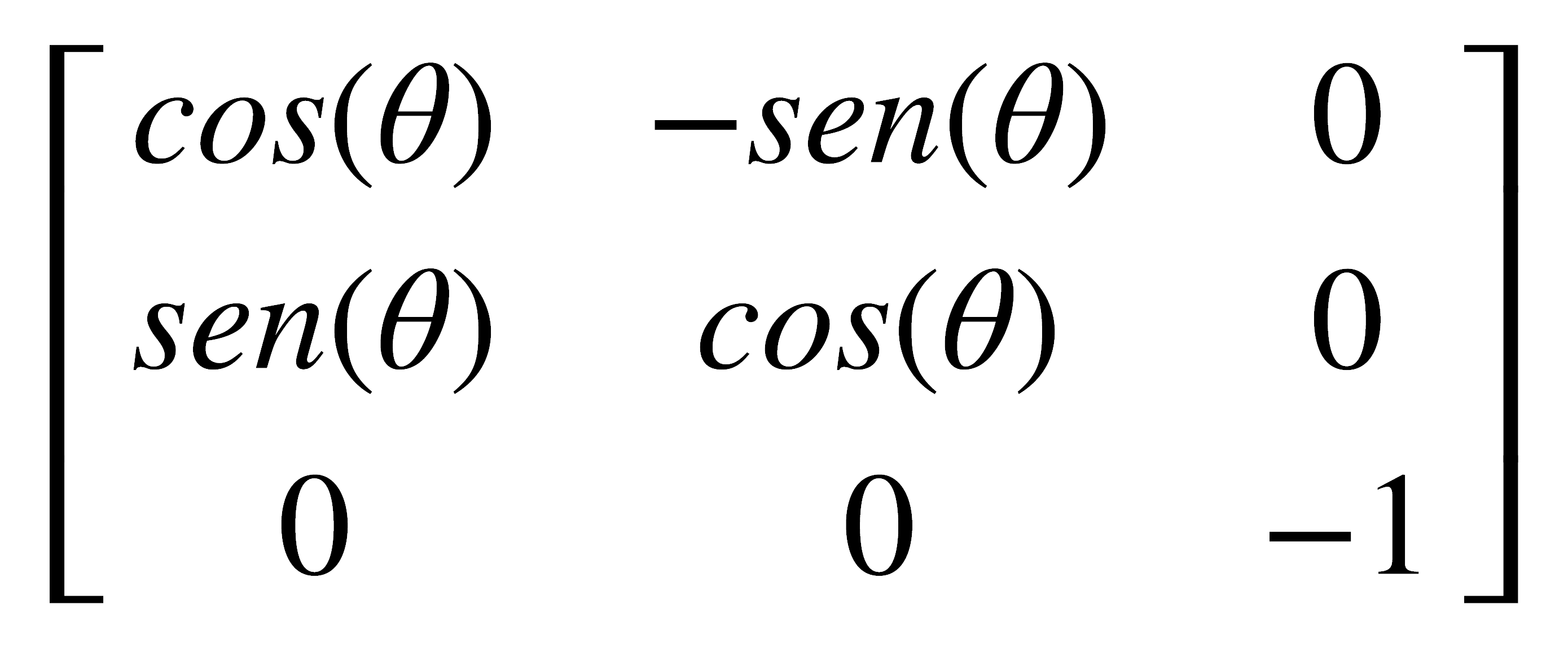
En general, la multiplicación de dos operaciones de simetría se reduce entonces a la multiplicación de las matrices que describen las operaciones, en el mismo orden.
Representaciones de los grupos puntuales
La representación de un grupo puntual puede hacerse a través del conjunto de matrices que representa las operaciones del grupo. Este conjunto de matrices satisface las propiedades de un grupo puntual. Por ejemplo, la representación del grupo C2v es la siguiente:
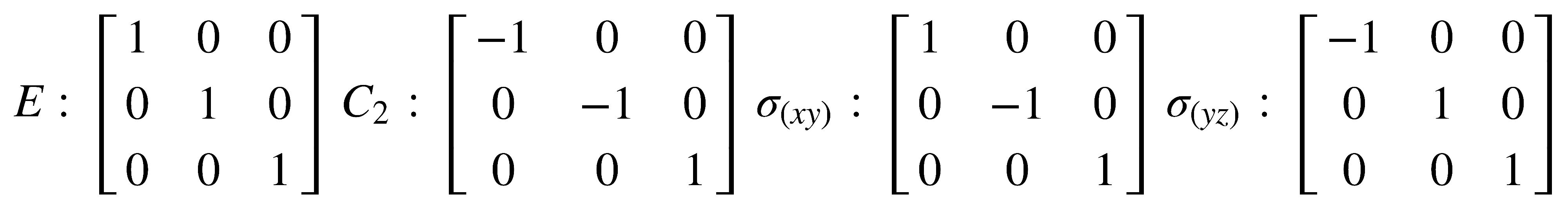
Para cada una de estas matrices puede hallarse su traza o carácter y el conjunto de éstos constituye también una representación del grupo. El carácter, definido únicamente para una matriz cuadrada es la suma de los números que se encuentran en la diagonal de la matriz, desde el extremo superior izquierdo hasta el inferior derecho. Por ejemplo, para el grupo C2v, se obtienen los siguientes caracteres:
| E | C2 | σv(xy) | σv(yz) |
| 3 | -1 | 1 | 1 |
Representaciones reducibles e irreducibles
Del ejemplo anterior se deduce que para un mismo grupo puede encontrarse un gran número de representaciones. Sin embargo, sólo un pequeño número de ellas tiene un significado fundamental. Cuando en una matriz los elementos que se encuentran fuera de la diagonal son iguales a cero, se dice que está "diagonalizada en bloque". La matriz puede entonces descomponerse en pequeñas matrices de 1x1 a lo largo de la diagonal y con ellas pueden conformarse otras Representaciones del grupo.
Si de las matrices que representan al grupo C2v se escriben independientemente los caracteres de las matrices 1x1 que tienen como base un cierto eje de coordenadas, se obtienen otras Representaciones del grupo, en las que cada fila tiene como base un solo eje de coordenadas:
| E | C2 | σv(xy) | σv(yz) | Coordenada usada | |
| 1 | -1 | 1 | -1 | x | |
| 1 | -1 | -1 | 1 | y | |
| 1 | 1 | 1 | 1 | z | |
| G | 3 | -1 | 1 | 1 |
Las tres primeras representaciones de las tabla anterior se denominan representaciones irreducibles, porque representan los caracteres de matrices diagonalizadas en bloque que ya no pueden descomponerse en partes más pequeñas. Estas representaciones irreducibles son las que tienen importancia fundamental en un grupo, y son las que se presentan en las tablas de caracteres, ya explicadas anteriormente.
Las representaciones irreducibles pueden combinarse en diferentes formas para dar lugar a representaciones reducibles, G. En general, un conjunto de matrices constituye una representación reducible cuando es posible transformar cada una de ellas mediante otra matriz, de manera que las nuevas matrices puedan separarse para dar una o varias representaciones de menores dimensiones. La manera de diagonalizar en bloque las matrices para obtener otras de menores dimensiones está fuera del alcance de este texto y puede consultarse en libros sobre teoría de grupos.
Si se tienen en cuenta las propiedades de las tablas de caracteres, es fácil notar que la tabla anterior no muestra todas las representaciones irreducibles del grupo C2v, puesto que si hay cuatro clases de operaciones de simetría, deben existir cuatro representaciones irreducibles. La representación faltante puede encontrarse fácilmente mediante el uso de otras propiedades de las tablas de caracteres. De acuerdo con la tercera propiedad, se requiere que la suma de los productos de los caracteres de dos representaciones cualesquiera sea igual a cero. Por lo tanto, si se utiliza la representación que toma como base la coordenada en z:
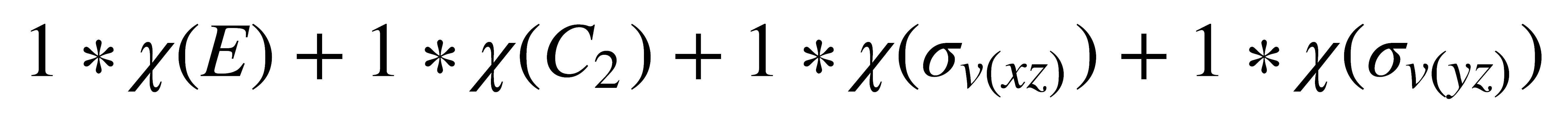
Para que la ecuación anterior se cumpla, dos de los caracteres de la representación desconocida deben ser iguales a +1 y dos a -1. Como c(E) =1 (por la primera propiedad) y no puede haber en una tabla de caracteres dos representaciones idénticas, se deduce que:
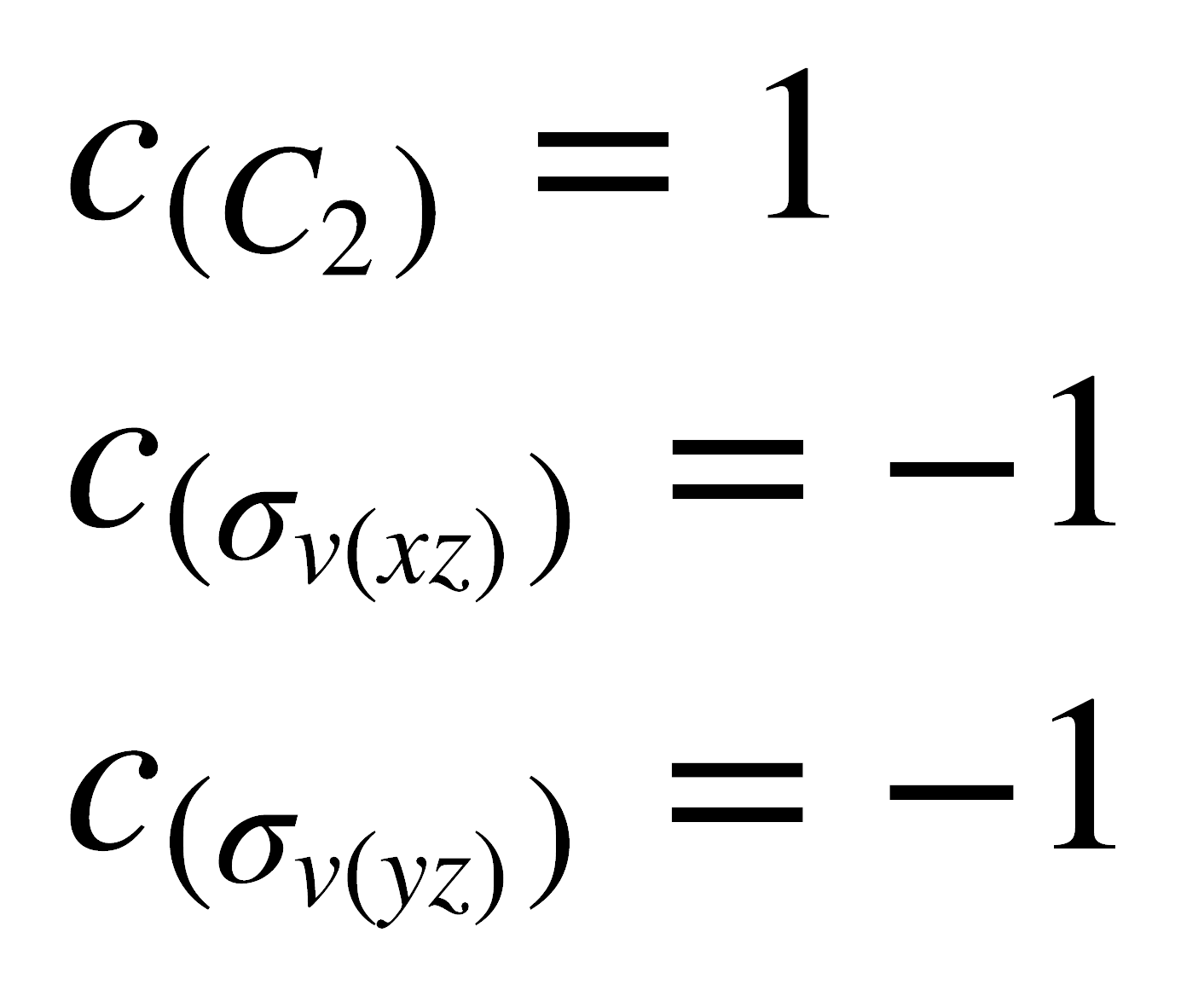
Reducción de representaciones reducibles a representaciones irreducibles.
La relación existente entre las representaciones reducibles y las irreducibles es de gran importancia, especialmente en la aplicación de la teoría de grupos a problemas específicos. Para separar una representación reducible en sus representaciones irreducibles componentes, se utiliza otra propiedad de los grupos. El número de veces que una representación irreducible está contenida en una representación reducible es igual a la suma de los productos de los caracteres de las representaciones reducibles e irreducibles por el número de operaciones de cada clase, dividida por el orden del grupo. En forma de ecuación, esto puede expresarse en la siguiente forma:
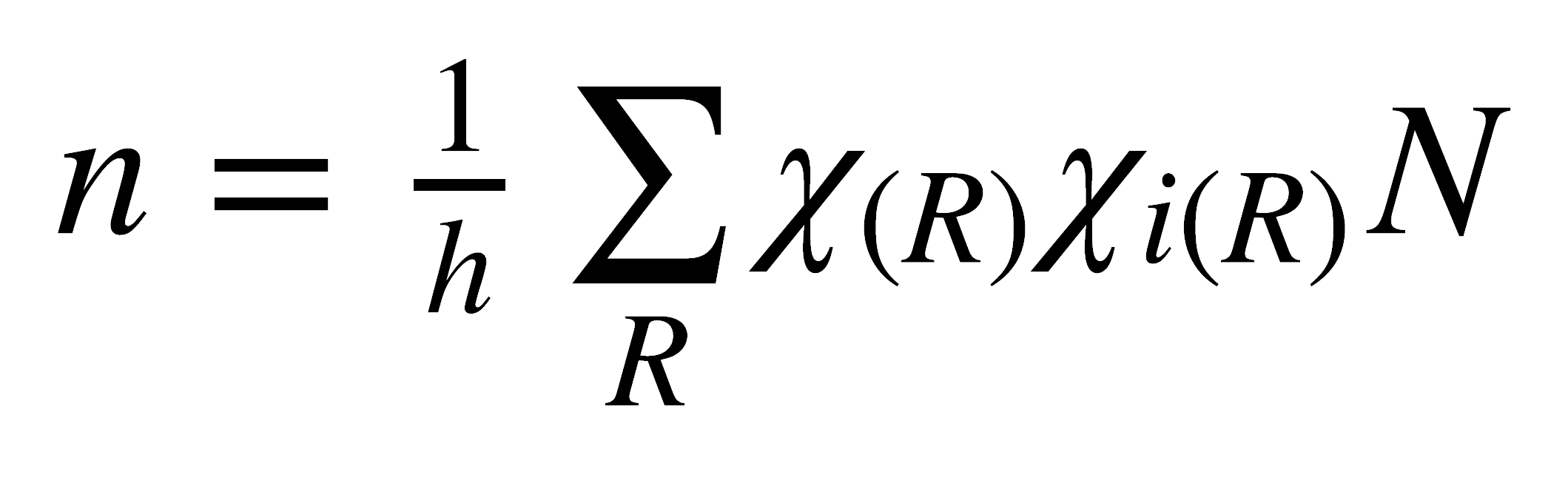
donde
- n = número de veces que aparece la representación irreducible
- h = orden del grupo
- χ(R) = Carácter de la representación reducible para la operación R
- χi(R) = Carácter de la representación irreducible para la operación R
- N = número de operaciones de cada clase
Este procedimiento debe dar un entero para el número de representaciones irreducibles de cada tipo, de lo contrario implica un error en los cálculos. Por ejemplo, teniendo en cuenta la tabla de caracteres completa del grupo C2v:
| C2v | E | C2 | σv(xy) | σv(yz) | |
| A1 | 1 | 1 | 1 | 1 | z |
| A2 | 1 | 1 | -1 | -1 | Rz |
| B1 | 1 | -1 | 1 | -1 | x, Ry |
| B2 | 1 | -1 | -1 | 1 | y, Rx |
En la representación reducible G (3 -1 1 1) encontrada anteriormente, las representaciones irreducibles componentes pueden determinarse así: