Funciones de onda tipo d
A los interesados se les presenta este adendum con algún desarrollo teórico de las funciones de onda orbital.
Los compuestos de coordinación de mayor interés son los que se forman con los iones de transición. Estos se caracterizan por presentar funciones orbitales de tipo d. Por esta razón, es conveniente recordar algunos puntos importantes sobre la densidad de carga, las funciones orbitales principales y sus representaciones gráficas.
Las gráficas tridimensionales descritas la mayoría de las veces como orbitales corresponden a una sobresimplificación del contorno exterior que busca encerrar el 90% de probabilidad acumulativa que se conoce sencillamente como densidad de carga, o probabilidad de densidad. Entre más internos son estos contornos, encierran una probabilidad de densidad más alta, pero una menor probabilidad de carga total.
La probabilidad de densidad de carga electrónica se puede encontrar elevando al cuadrado las funciones de onda electrónicas. Las funciones de onda electrónicas hidrogenoides, comúnmente conocidas como orbitales, constan de una parte radial y de otra angular, cada una de las cuales se puede graficar. Existe una dificultad para graficar la parte angular de las funciones del hidrógeno en coordenadas polares ya que éstas involucran números complejos, entonces se trabaja con el módulo, que es un número real.
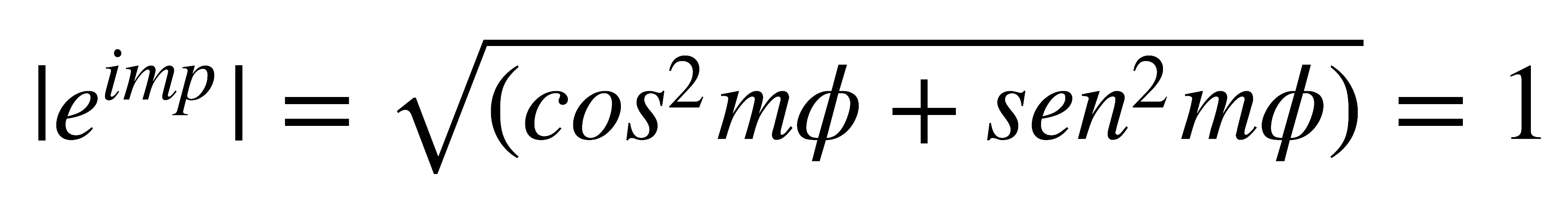
Para las funciones p+1 y p-1, en las cuales m=0, las funciones angulares son:
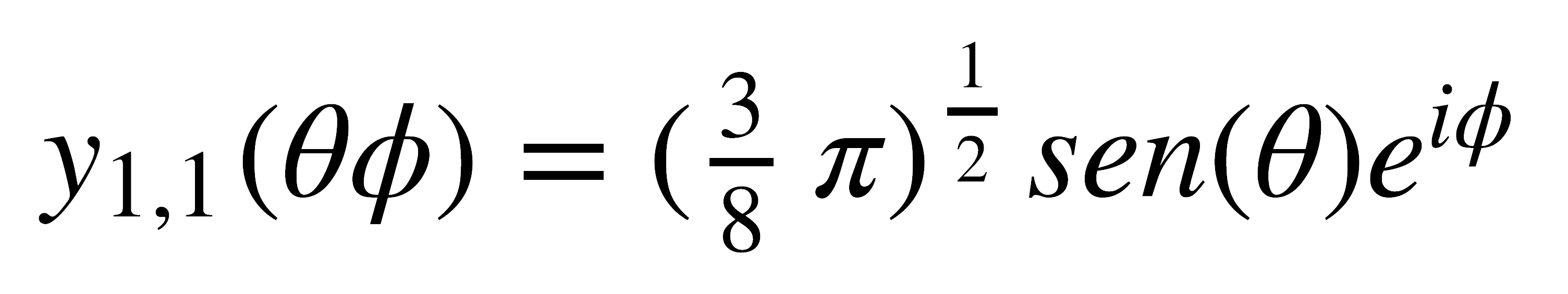

Aplicando la primera ecuación, el módulo de ambas funciones es idéntico:
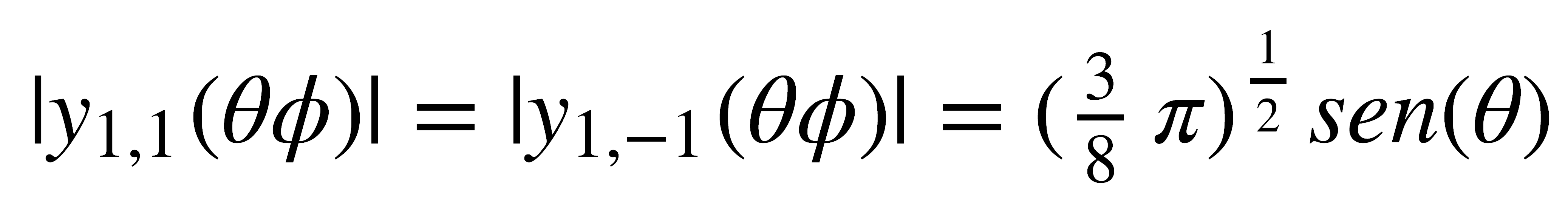
que es una función fácilmente graficable.
Se acostumbra analizar las partes angulares haciendo combinaciones de las funciones complejas para obtener funciones de valor real fácilmente graficables, conocidas como armónicos esféricos reales normalizados (aern). Estas nuevas funciones están caracterizadas solamente por el número cuántico l y por la paridad (sen o cos) de la función de ɸ, y corresponden únicamente a un valor de ½m ½. Los aern reciben un nombre por la forma que adquieren al ser expresados en coordenadas cartesianas.
En siguiente tabla se presentan las funciones angulares del hidrógeno y sus armónicos esféricos reales normalizados (aern) para las orbitales s, p y d.
| Función* | l | ml | Nombre | Función angular | Armónicos esféricos reales normalizados |
| y(0,0) | 0 | 0 | s | (1/4p)1/2 | (1/4p)1/2 |
| y(1,0) | 1 | 0 | Pz | (3/4p)1/2cosθ | (3/4p)1/2cosθ |
| y11, cos | 1 | 1 | Px | (3/8p)1/2senθ eiφ | (3/8p)1/2senθ eiφ |
| y11, sen | 1 | -1 | Py | (3/8p)1/2senθ e-iφ | (3/8p)1/2senθ e-iφ |
| y(2,0) | 2 | 0 | dz2 | (5/16p)1/2(3cosθ2-1) | (5/16p)1/2(3cosθ2-1) |
| y12,cos | 2 | 1 | dxy | (15/8p)1/2senθ cosθ eiφ | (15/4p)1/2senθ cosθ cosφ |
| y12,sen | 2 | -1 | dyz | (15/8p)1/2senθ cosθ e-iφ | (15/4p)1/2senθ cosθ senφ |
| y22,cos | 2 | 2 | dx2y2 | (15/32p)1/2sen2θ e2iφ | (15/16p)1/2sen2θ cos2φ |
| y22,sen | 2 | -2 | dxy | (15/32p)1/2sen2θ e-2iφ | (15/16p)1/2sen2θ sen2φ |
Los superíndices se refieren a |m|
En la tabla anterior puede notarse que en las funciones con m=0 los aern corresponden a las mismas funciones angulares puesto que son valor real.