Tablas de multiplicar y proyecciones estereográficas

Resumen: Las operaciones de simetría son elementos de un grupo matemático. Con el fin de comprobar que estas operaciones si cumplen con las leyes de los grupos matemáticos se desarrollan las tablas de multiplicar, combinaciones de operaciones de simetría. Las proyecciones estereográficas facilitan encontrar el producto de una combinación.

En simetría es de gran importancia representar el efecto neto de aplicar una operación de simetría inmediatamente después de otra, ya que esto determina una serie de propiedades que se verán más adelante. La forma de representar la operación X se lleva a cabo primero y a continuación se efectúa la operación Y, produciendo el mismo efecto neto que si se hubiera aplicado únicamente la operación Z.

Y x X = Z

Puede notarse que el orden de aplicación de las operaciones es de derecha a izquierda, lo cual debe tenerse muy en cuenta porque en general el resultado cambia según el orden en que se apliquen las operaciones. La manera normal de referirse a esta combinación de operaciones es como el producto de ellas. Muchas veces, la existencia de una o varias operaciones de simetría implica la existencia de otras. Esto se comprueba fácilmente haciendo el producto de las dos operaciones, ya que la multiplicación de dos operaciones de simetría en una molécula da como resultado otra operación de simetría de la molécula. Por ejemplo, para la molécula de H₂O, las operaciones de simetría son E, C₂, σ_v1 y σ_v2, tal como se ilustra a continuación:

En esta molécula el resultado de la multiplicación C₂ x σ_v2 será la operación equivalente a efectuar primero una reflexión sobre σ_v2 y a continuación, sobre el resultado de esta operación, efectuar una rotación de 180° sobre C₂; entonces, esta combinación corresponde a efectuar σ_v1.

La multiplicación de operaciones de simetría puede representarse mediante la tabla de multiplicar. En ella se indican todas las operaciones de simetría en el mismo orden, tanto en la fila superior como en la columna de la izquierda. En la intersección se escribe el resultado del producto de las operaciones, realizando en primer lugar la operación indicada en la fila superior y a continuación la de la columna de la izquierda. Por ejemplo, para la molécula de agua, las letras A, B, C, D representarían:

	E	C2	σv1	σv2
E		A
C2			B
σv1	C			D
σv2

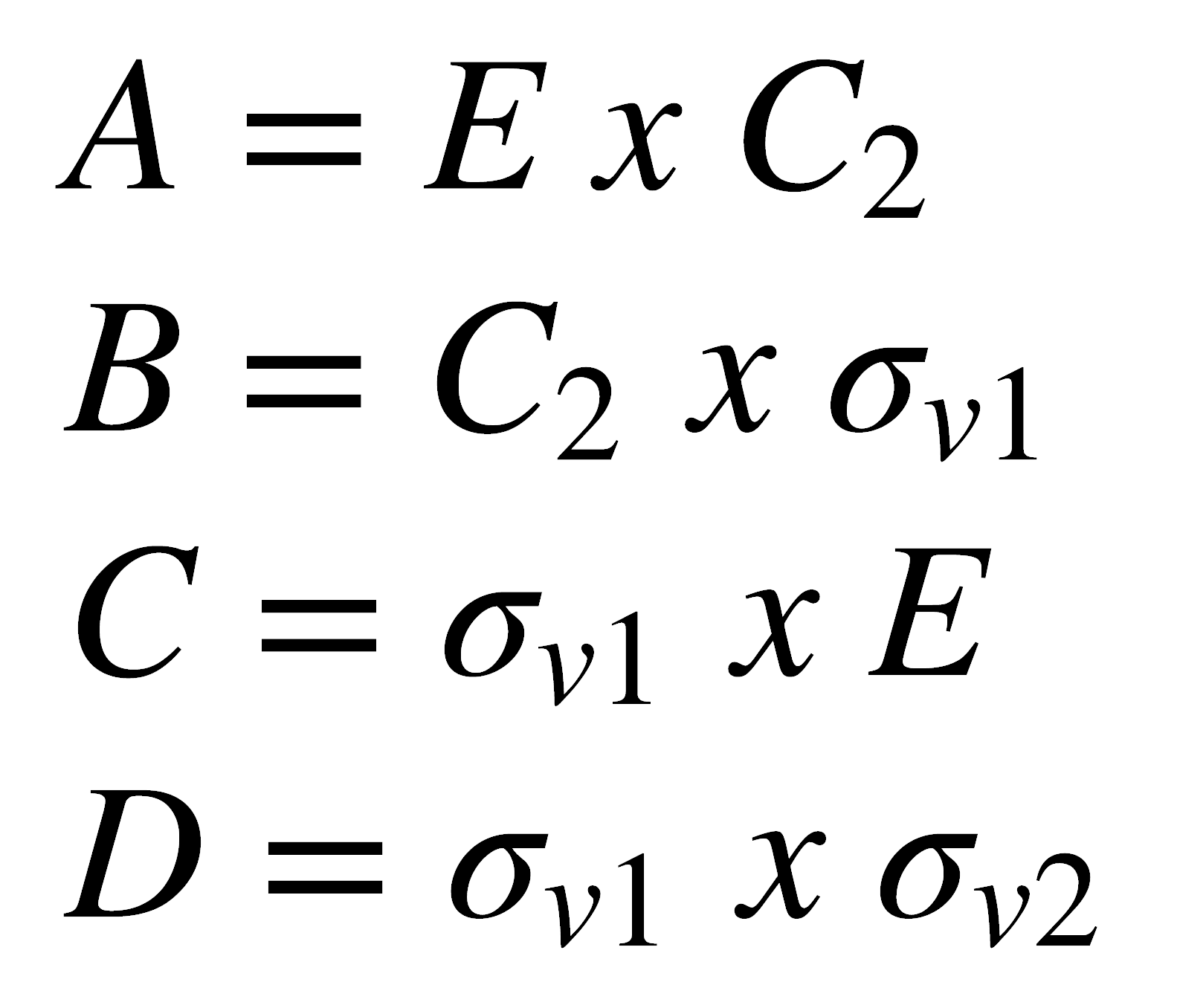
No siempre es fácil deducir rápidamente el resultado de la multiplicación de operaciones de simetría. Esta tarea se simplifica grandemente al elaborar una proyección estereográfica. En ella se representa la proyección de todos los elementos de simetría de la molécula en un plano y luego se representan las proyecciones de todos los puntos generados por las operaciones de simetría realizadas sobre un punto imaginario, es decir, que no representa ningún átomo específico de la molécula.

Las proyecciones estereográficas son de gran utilidad para realizar la multiplicación de operaciones de simetría, ya que el resultado, al ser operación de simetría de la molécula, está representado en ellas mismas. Por otra parte, la proyección estereográfica debe ser simétrica, lo cual es útil para encontrar relaciones entre las operaciones de simetría.

Para la representación de los diferentes elementos de simetría se supone que la molécula está situada dentro de una esfera hueca, con su centro de gravedad en el centro de la esfera. Todos los planos y ejes de simetría tendrán una intersección común en el centro. A continuación se proyectan sus intersecciones sobre el plano ecuatorial de la esfera; en esta forma, el plano horizontal de la molécula debe coincidir con el plano ecuatorial. Si éste existe, se dibuja con una línea continua, en caso contrario, se dibuja con línea punteada. El eje de mayor orden sería perpendicular a este plano y atravesaría la esfera por el centro, por lo tanto se indica en el centro de la circunferencia dibujada mediante un pequeño polígono cuyo número de lados indica el orden del eje. El eje propio se representa rellenando el polígono, y el impropio, únicamente con el contorno. Por ejemplo, un eje propio de orden 2 se representa como () y el de orden tres como △; el eje impropio de orden 3 se representa como ▲.

Al proyectar un plano de simetría vertical resulta una línea, luego éste se indica con una línea continua. Un eje de simetría perpendicular al eje de mayor orden no da lugar a proyección puesto que atraviesa la esfera por el círculo ecuatorial. Se representan entonces los puntos de intersección mediante polígonos llenos con tantos lados como sea el orden del eje, unidos por una línea discontinua. El centro de simetría se halla también en el plano ecuatorial, por lo tanto no se puede proyectar; éste se representa como el eje S₂, ya que son equivalentes. Cuando los elementos de simetría tienen una orientación arbitraria son más difíciles de representar y se encuentran fuera del alcance de este curso. La persona interesada puede consultar los libros de la bibliografía recomendada.

La representación de los principales elementos de simetría en una proyección estereográfica (C₃, σ_v1, σ_v2, σ_v3) se ilustran a continuación:

Hasta el momento se ha considerado la representación de los elementos de simetría sobre el plano ecuatorial de la esfera. El paso siguiente es la representación de las operaciones de simetría. Para ello se coloca un punto en cualquier parte de la proyección estereográfica, que preferiblemente no se encuentre sobre ninguno de los elementos de simetría, y sobre él se realizan todas las operaciones de simetría de la molécula. Si el punto considerado corresponde al hemisferio de la esfera que se encuentra sobre el plano de proyección, se representa en éste por una cruz (X), y si corresponde al hemisferio que se encuentra bajo el plano de proyección, se representa por un círculo (O). Lo anterior puede ilustrarse con la proyección estereográfica de la molécula de agua.

---

---

	E	C2	σv1	σv2
E	E	C2	σv1	σv2
C2	C2	E	σv2	σv1
σv1	σv1	σv2	E	C2
σv2	σv2	σv1	C2	E

E x E = E	σv1 x E = σv1
E x C2 = C2	σv1 x C2 = σv2
E x σv1 = σv1	σv1 x σv1 = E
E x σv2 = σv2	σv1 x σv2 = C2
C2 x E = C2	σv2 x E = σv2
C2 x C2 = E	σv2 x C2 = σv1
C2 x σv1 = σv2	σv2 x σv1 = C2
C2 x σv2 = σv1	σv2 x σv2 = E

Pueden observarse aspectos interesantes en esta tabla de multiplicar. En primer lugar, ninguna operación se repite a lo largo de una fila ni de una columna. De esto se desprende que no pueden haber dos filas ni dos columnas idénticas. Por otra parte, el resultado de multiplicar cualquier operación por la identidad, o viceversa, es la misma operación, luego la primera fila y la primera columna son las mismas operaciones escritas en los encabezamientos de la tabla.

Consideremos ahora el trans-[PtCl₂(NH₃)₂], cuyas operaciones de simetría son: E, C₂, C₂₁, C₂₂, i, σ_h, σ_v1, σ_v2.

---

---

La tabla de multiplicar correspondiente es:

	E	C2	C21	C22	i	σh	σv1	σv2
E	E	C2	C21	C22	i	σh	σv1	σv2
C2	C2	E	C22	C21	σh	i	σv2	σv1
C21	C21	C22	E	C2	σv2	σv1	σh	i
C22	C22	C21	C2	E	σv1	σv2	i	σh
i	i	σh	σv2	σv1	E	C2	C22	C21
σh	σh	i	σv1	σv2	C2	E	C21	C22
σv1	σv1	σv2	σh	i	C22	C21	E	C2
σv2	σv2	σv1	i	σh	C21	C22	C2	E

Para conocer más acerca de las interacciones con los modelos dinámicos de moléculas y obtener más información acerca de JSmol, puede dirigirse a la página de Ayuda

Aviso importante: Es posible que en algunos dispositivos y pantallas de baja resolución algunas de las moléculas dinámicas se visualicen de forma superpuesta, o que sus marcos se traslapen. Para solucionar ese inconveniente se debe usar la función de alejamiento que está disponible en cualquier navegador. Esta función se activa en Windows y Linux con las teclas CTRL y -, y en iOS con las teclas ⌘ y -.