Teoría del campo cristalino (I)
Resumen: La TCC la desarrollaron los físicos Bethe y Van Vleck. Es una teoría electrostática centrada en la interacción entre los orbitales d del ión central y los átomos donores de los ligantes. Se parte del principio de que los orbitales d del ión central en ausencia de ligantes tienen la misma energía, son o están degenerados, cuando los ligantes se acercan al ión central apuntan más hacia unas densidades d que hacia otras, los afectados por los ligantes aumentan su energía, los otros la disminuyen, se desdobla la energía, se forma una diferencia de energía entre ellas. Esta diferencia de energía es la base para explicar el color de los compuestos de coordinación. El modelo explica el magnetismo, el color y otras propiedades de los compuestos de coordinación. (Una discusión TEV vs. TCC se presentará en un blog del autor).
La teoría del Campo Cristalino fue desarrollada por Bethe y Van Vleck aproximadamente en la misma época que la teoría de enlace de valencia. Sin embargo, el haber sido propuesta por físicos contribuyó a que permaneciera ignorada por los químicos aproximadamente hasta 1950. A partir de ese momento tomó auge porque explicaba algunos hechos que no podían serlo por la Teoría de Enlace-Valencia, tales como el color de los compuestos de coordinación. La principal ventaja que presenta la teoría de campo cristalino es que es conceptualmente muy sencilla y está basada en argumentos de simetría similares a los de la teoría de orbitales moleculares.
La teoría se basa en suponer que existe una interacción puramente electrostática entre los ligantes y el ión metálico central, es decir, se excluye cualquier posibilidad de covalencia. Los enlaces metal - ligante se describen como el resultado de la atracción entre los iones metálicos positivos y los ligantes negativos cargados, o al menos, con el extremo negativo de ligantes polares.
Para entender la teoría del campo cristalino, es necesario tener una imagen mental muy clara de la orientación espacial de las densidades electrónicas de las orbitales d, ya que es la interacción de éstas con los ligantes la que produce los efectos por campo cristalino.
Densidad monoelectrónica dxy
Para interactuar coloque el mouse sobre la gráfica
Densidad monoelectrónica dxz
Para interactuar coloque el mouse sobre la gráfica
Densidad monoelectrónica dyz
Para interactuar coloque el mouse sobre la gráfica
Densidad monoelectrónica dx2-y2
Para interactuar coloque el mouse sobre la gráfica
Densidad monoelectrónica dz2
Para interactuar coloque el mouse sobre la gráfica
La energía de los cinco orbitales d en un ión metálico gaseoso y aislado es degenerada; pero, si un campo esféricamente simétrico de cargas negativas se coloca alrededor del ión metálico, la energía de los orbitales aumentará como consecuencia de la repulsión entre el campo negativo y los electrones descritos por las funciones orbitales, pero permanecerán aún degeneradas. Si el campo negativo se produce ahora por la influencia de ligantes reales, la simetría no es esférica sino menor porque el número de ligantes es finito.
Desdoblamiento de los orbitales d en un campo octaédrico
Consideremos ahora el caso de seis ligantes que se aproximan para formar un complejo octaédrico. Por conveniencia, supondremos que éstos se encuentran sobre los ejes de coordenadas cartesianas en las direcciones x, -x, y, -y, z, -z, en la forma que se muestra a continuación:
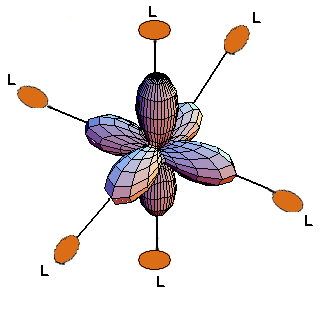
En estas condiciones los ligantes interactúan fuertemente con las orbitales dz2 y dx2 -y2, cuya densidad electrónica se encuentra sobre los ejes de coordenadas. Por simetría este grupo de orbitales se conoce como eg. Al ser fuerte la interacción con los ligantes, los orbitales aumentan su energía. Por otra parte, el grupo de las orbitales dxy, dxz y dyz, conocido como t2g, disminuye su energía porque la densidad electrónica se presenta entre los ligantes. Esta transformación de los cinco orbitales degenerados en dos grupos de orbitales con diferente energía es la base de la teoría de campo cristalino y se conoce como desdoblamiento por campo cristalino. La diferencia de energía que separa estos dos grupos de orbitales se conoce como 10 Dq. Esta cantidad puede ser grande o pequeña, pero en cualquier caso es 10 Dq por definición.
En el desdoblamiento de los orbitales d, el centro de gravedad de la energía permanece constante. Para que esto se cumpla, la energía promedio de los orbitales eg debe aumentar en un valor de 6 Dq, mientras que la energía de las orbitales t2g debe disminuir en un valor de 4 Dq.
Desdoblamiento de los orbitales y el centro de gravedad de la energía
De esta forma, los electrones del ión metálico tienden a tener la menor energía posible, lo cual se logra porque los primeros electrones van al nivel energético t2g, en donde por cada electrón habrá una estabilización de 4 Dq.
El valor de energía neto en que se estabiliza un complejo se denomina energía de estabilización por campo cristalino (EECC). Para estas configuraciones se cumple la regla de Hund, la cual afirma que en un mismo nivel energético los electrones deben permanecer desapareados. Sin embargo, después de la configuración d3 el nivel t2g está semilleno y no hay más orbitales libres de esta energía.
En el caso de una configuración d4 surgen dos posibilidades: cuando el valor de 10 Dq o abertura de campo es pequeño con relación a la energía de apareamiento de los electrones, el cuarto electrón se ubica en una de las orbitales eg. No obstante, se pierde algo de energía de estabilización por campo cristalino debido a que cada electrón de los orbitales eg desestabiliza el complejo en una cantidad correspondiente a 6 Dq. Cuando esto sucede se dice que el campo cristalino es débil. Los complejos de campo débil se conocen también con el nombre de complejos de espín alto por cuanto en ellos se presenta siempre el mayor número de electrones desapareados.
Por otra parte, para una configuración d4 surge otra posibilidad, la cual ocurre cuando la abertura de campo es grande, campo fuerte, y esta diferencia de energía (10 Dq) es mayor que la energía de apareamiento. En este caso, para el ion d4, el cuarto electrón se aparea en el nivel t2g en lugar de pasar al nivel eg. La EECC será entonces de 16 Dq (4*4Dq), y el momento magnético será 2.7 MB, indicativo de dos electrones desapareados y el ion será de espín bajo.
La configuración d5 en un campo débil, t2g3 eg2, posee una energía de estabilización por campo cristalino de cero, por lo cual los dos subniveles eg están semillenos y la energía de estabilización del subnivel t2g está perfectamente balanceada por la energía de desestabilización del nivel eg. En otras palabras, la configuración d5 en un campo débil es esféricamente simétrica y no ocurre estabilización por la aplicación de un campo octaédrico.
En general, un campo cristalino fuerte corresponde a una abertura de campo cristalino grande con respecto a la energía de apareamiento de los electrones y como resultado es más favorable en las configuraciones d4 a d6.
Campo fuerte
Campo débil
La energía de estabilización por campo cristalino en un complejo de campo fuerte es mayor con respecto a las mismas configuraciones d en un campo débil, observándose una disminución de ésta a partir de la configuración d7 debido a que estos electrones pertenecen al nivel eg.
Estos compuestos se conocen también con el nombre de complejos de espín bajo, ya que al presentarse apareamiento de los electrones, el espín total del ion metálico es el más bajo posible.
Desdoblamiento por campos octaédricos
Fig. 5.24 Desdoblamiento por Campos Octaédrico
La siguiente tabla muestra la energía de estabilización por campo cristalino resultante para cada configuración tanto en un campo octaédrico débil como en uno fuerte, y el número de electrones desapareados que se espera para cada una de ellas. Es de anotarse que como la EECC siempre estabiliza un complejo, debe expresarse como una cantidad negativa, pero en la práctica se ha perdido el signo negativo y las EECC aparecen listadas como positivas. Esto no debe causar confusión desde que se recuerde que EECC < 0.
| Campo débil | Campo fuerte | ||||
| t2g1 | 4 Dq | t2g1 | 4 Dq | ||
| t2g2 | 8 Dq | t2g2 | 8 Dq | ||
| t2g3 | 12 Dq | t2g3 | 12 Dq | ||
| t2g3 eg1 | 6 Dq | t2g4 | 16 Dq | ||
| t2g3 eg2 | 0 Dq | t2g5 | 20 Dq | ||
| t2g4 eg2 | 4 Dq | t2g6 | 24 Dq | ||
| t2g5 eg2 | 8 Dq | t2g6 eg1 | 18 Dq | ||
| t2g6 eg2 | 12 Dq | t2g6 eg2 | 12 Dq | ||
| t2g6 eg3 | 6 Dq | t2g6 eg3 | 6 Dq | ||
| t2g6 eg4 | 0 Dq | t2g6 eg4 | 0 Dq | ||
Es común referirse a la EECC únicamente en términos de Dq, aunque se sobreentiende que para configuraciones de d5 en adelante en el caso del campo débil y en d3 en adelante en el caso del campo fuerte hay disminución en ésta debido a la energía de apareamiento. En los textos en que este parámetro se incluye, aparece solamente en el caso del campo fuerte ya que generalmente se mide a partir del cambio en el número de pares de electrones al pasar del campo débil al campo fuerte.
La importancia de la teoría de campo cristalino se debe en gran parte a la explicación que ofrece para la presencia del color en los compuestos de coordinación con metales de transición. Una consecuencia de las relativamente pequeñas diferencias de energía entre los orbitales d no equivalentes (10 Dq) es que un electrón puede excitarse de los niveles de menor energía a los de mayor energía simplemente por absorción de luz visible. Como esta absorción corresponde a una absorción de una longitud de onda determinada, habrá longitudes de onda correspondientes a otras regiones del espectro visible que no son alteradas y corresponden al color observado para el compuesto.
Esta es una explicación bastante simplificada, ya que cuando los complejos contienen más de un electrón d aumenta el número de transiciones electrónicas posibles. Estas transiciones que ocurren entre orbitales d del ión central se conocen con el nombre de transiciones d -d, o de campo ligando.
El ejemplo más sencillo es el del ion [Ti(H2O)6]3+, puesto que el ion Ti3+ tiene una configuración electrónica d1, que en el caso del complejo octaédrico corresponde a una t2g1. Este complejo es de color violeta, lo que implica que absorbe luz en la región visible.
La absorción que se presenta en el complejo a 500nm se explica por la transición electrónica t2g1 eg0 -> t2g0 eg1
Desdoblamiento de los orbitales d en un campo tetraédrico
Otra geometría común en los complejos de los metales de transición, es la tetraédrica, la cual está estrechamente relacionada con una geometría cúbica debido a que un tetraedro puede inscribirse dentro de un cubo.
En esta distribución ninguno de los ligantes está directamente orientado hacia alguna de los orbitales d, aunque están más cerca de los orbitales dxy, dxz, dyz, que de los orbitales dz2 y dx2-y2. Es decir, que los ligantes se encuentran más próximos a las aristas del cubo que a los centros de las caras del mismo. Por consiguiente, las orbitales d se desdoblan en dos grupos: e y t2 cuyo desdoblamiento es invertido con respecto al campo octaédrico.
La abertura del campo por campo tetraédrico es aproximadamente 4/9 de la correspondiente a un campo octaédrico, como consecuencia de la orientación de los ligantes y las orbitales d; por lo cual no se conocen complejos tetraédricos de campo fuerte.