Teoría del enlace de valencia
Resumen: La TEV se debe a Linus Pauling. Más conocida como modelo de las hibridaciones o de los orbitales híbridos, modelo muy utilizado en química orgánica en donde las discusiones se dan en términos de los híbridos sp, sp2 o sp3 del carbón en referencia. Linus Pauling amplía su teoría para aplicarla a los compuestos de coordinación con iones de transición, es decir con participación de las orbitales d en la hibridación, además de las s y p. En el caso de los compuestos de coordinación la hibridación se hace con participación solo de lss “orbitales desocupadss” de menor energía, las LUMO. La TEV explica el magnetismo y la geometría de los compuestos de coordinación.
Esta teoría fue inicialmente propuesta por Linus Pauling en 1933 para explicar la dirección de los enlaces en los compuestos. La teoría está basada en el postulado de que la fuerza de un enlace depende de la distribución angular de las funciones orbitales involucradas.
Uno de los hechos que llevó a postular esta teoría es que el carbono, en vez de formar tres enlaces a ángulos rectos y formar otro más débil, forma cuatro enlaces equivalentes y dirigidos hacia los vértices de un tetraedro regular. De aquí se deriva que los orbitales 2s y 2p del carbono no son usados directamente en la formación de los enlaces.
En general la función de onda para un sistema puede construirse combinando otras funciones. La función de onda del estado fundamental es la que minimiza la energía del sistema. Para el caso del carbono, los cálculos demuestran que una función orbital de enlace formada por combinación lineal de las orbitales s y p en una cierta proporción de coeficientes numéricos, tiene una fuerza de enlace mayor que la de las orbitales s y p puras. La densidad electrónica de esta nueva función orbital está fundamentalmente concentrada en la dirección de los enlaces, por lo tanto la superposición con el orbital de otro átomo sería alta y formaría un enlace fuerte. Esta combinación lineal de funciones orbitales de un mismo átomo es la que se conoce como hibridación.
Estos mismos principios pueden aplicarse para explicar el enlace en los compuestos de coordinación. La principal característica en este caso es que los orbitales híbridos tienen gran contribución de orbitales d. En general, para átomos del tercer período en adelante, la diferencia de energía entre los orbitales s, p y d es lo suficientemente pequeña, de modo que estos tres tipos de funciones toman parte en la formación de los enlaces. Aún en compuestos que no son de coordinación, tales como PF5, PF3Cl2, PCl5, SF6, se pueden utilizar uno o dos orbitales d en la formación de los enlaces.
Sin embargo, en los complejos de los metales de transición, las orbitales d que normalmente intervienen en la formación de los enlaces son aquellas que tienen el número cuántico principal una unidad menor que el de la capa de valencia, debido a que los orbitales d internos tienen aproximadamente la misma energía que los orbitales s y p de la capa de valencia.
Complejos octaédricos
En el caso de los metales de transición en los compuestos de coordinación, deben hibridizarse tantas orbitales atómicas como se necesiten para acomodar los pares libres de los ligantes. Por ejemplo, en el [Fe(CN)6]4-:
| Fe [Ar] | 4s2 3d6 |
| Fe2+ [Ar] | 3d6 |
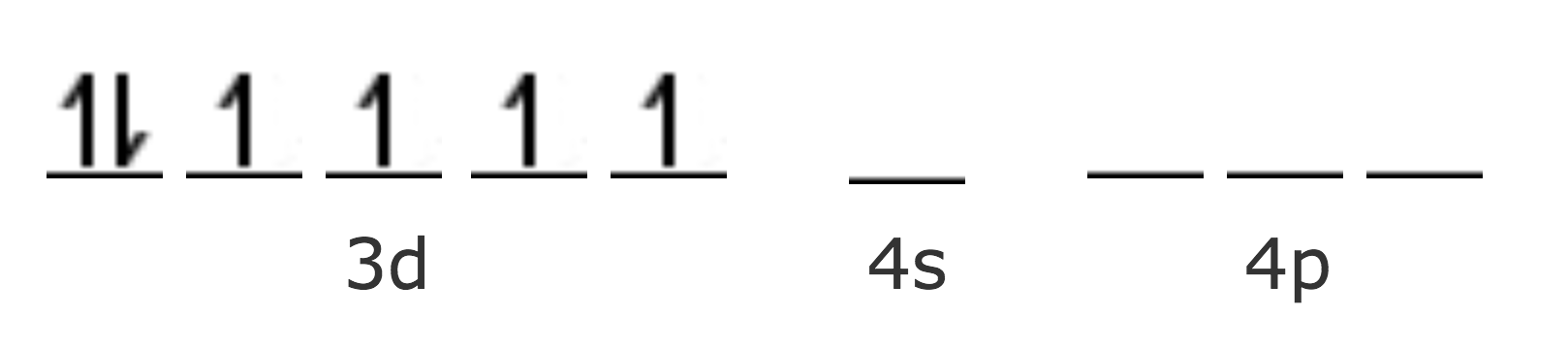
Para acomodar los seis ligantes se necesitan seis orbitales híbridos vacíos del ión metálico, por lo tanto debe suceder una reacomodación de los electrones del ión central.
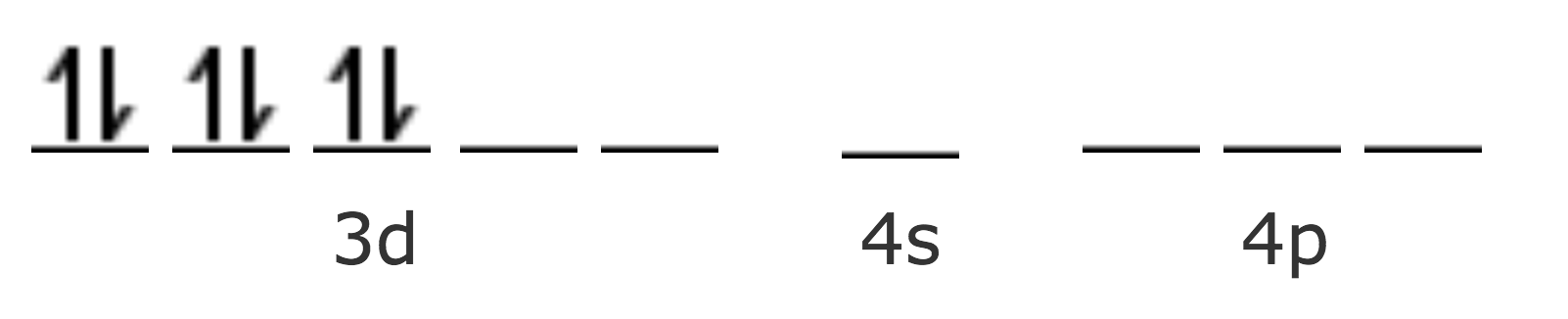
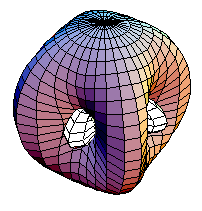
Estos seis orbitales híbridos tienen su mayor densidad de probabilidad orientada hacia los vértices de un octaedro, y por lo tanto puede concluirse que los compuestos hexacoordinados deben ser octaédricos. La gráfica de una de estas nuevas funciones de onda se a continuación:

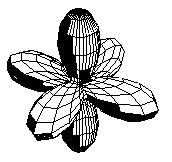
Orbitales híbridos d2sp3
Otro criterio importante utilizado en esta teoría es el de las propiedades magnéticas. En el caso del [Fe(CN)6]4-, al estar apareados todos los electrones del Fe2+, el compuesto es diamagnético.
En el [Fe(CN)6]3-:
| Fe3+ [Ar] | 3d5 |
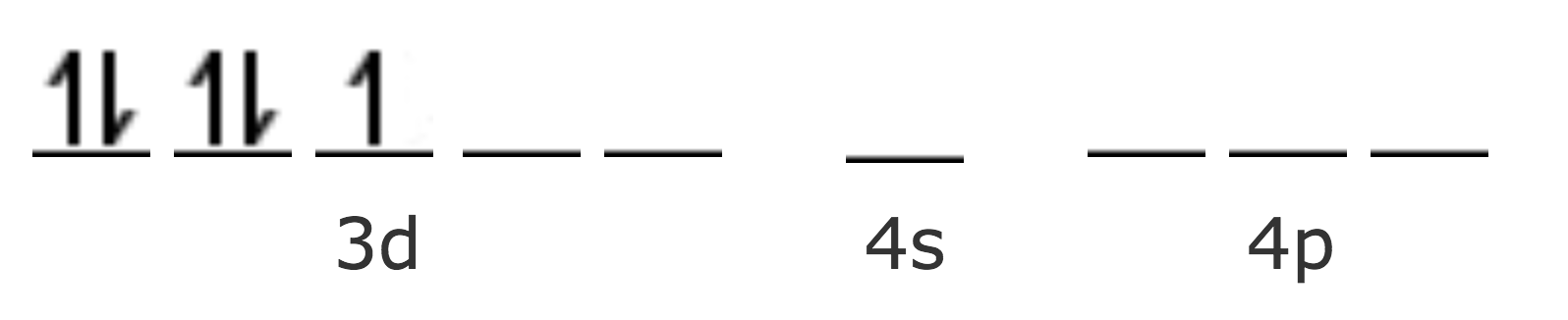
Este ion es paramagnético puesto que presenta un electrón desapareado. En el caso de los complejos octaédricos, cuando las orbitales 3d no están disponibles para la formación de las orbitales híbridas, entonces se pueden utilizar las orbitales 4d. En el primer caso, los ligantes están más fuertemente unidos al ión central, los enlaces son esencialmente covalentes y se conocen como complejos hiperligados, es decir de unión fuerte. Por otra parte, en el segundo caso, los enlaces tienen mayor carácter iónico, los ligantes están más débilmente unidos y por lo tanto se conocen como complejos hipoligados ó de unión débil.
El criterio magnético puede usarse para diferenciar entre estas dos clases de complejos. El momento magnético μ del [FeF6]3 es de aproximadamente 5.9 MB, como corresponde a cinco electrones desapareados, mientras que en el [Fe(CN)6]3 μ = 1.9 MB, correspondiente a un electrón desapareado.
Otro aspecto importante que permite explicar la teoría es la mayor estabilidad de los complejos hexacoordinados de Co III con respecto a los de Co(II).
| Co Z=27 [Ar] | 4s2 3d7 |
| Co2+ [Ar] | 3d7 |
| Co3+ [Ar] | 3d6 |
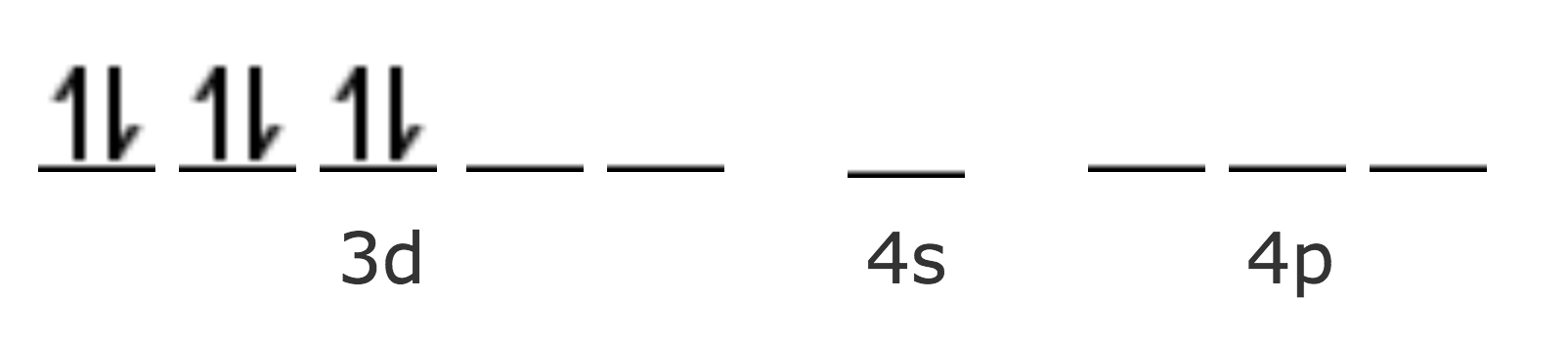

En el Co2+, el séptimo electrón se presenta en una orbital de mayor energía (4d), haciendo que el complejo sea inestable, por lo tanto puede oxidarse fácilmente a Co3+.
Complejos con otra geometría
En los complejos cuadrados planares deben hibridizarse cuatro orbitales del ión metálico para formar el enlace con los ligantes. Estas son la orbital 4s, dos 4p y una 3d. Al combinarlos se obtienen cuatro orbitales híbridas cuyas densidades de probabilidad están dirigidas hacia los vértices de un cuadrado. Las funciones de onda resultantes son:
Para la formación de estas orbitales híbridas sólo se usan dos de los orbitales p.
Por ejemplo, en el [Ni(CN)4]2-
| Ni Z=28 [Ar] | 4s2 3d8 |
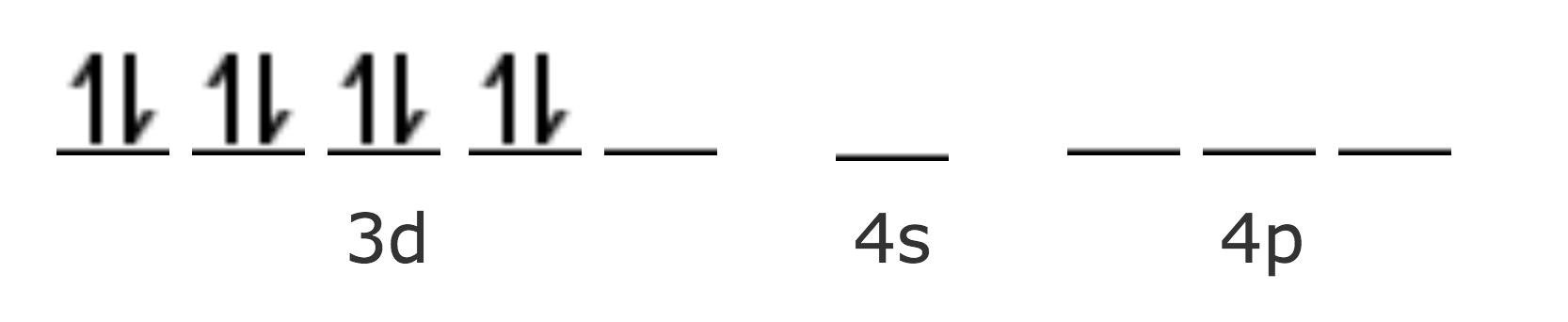
| Ni2+ [Ar] | 3d8 |

Orbitales híbridos dsp2
En este caso, el complejo es diamagnético. Sin embargo, se encuentran otros complejos de Ni2+ en los que μ = 2.83 MB, como por ejemplo el [Ni(NH3)4]2+, o el [NiCl4]2- . Este paramagnetismo puede explicarse con la hibridación sp3 a la que corresponde una estructura tetraédrica.
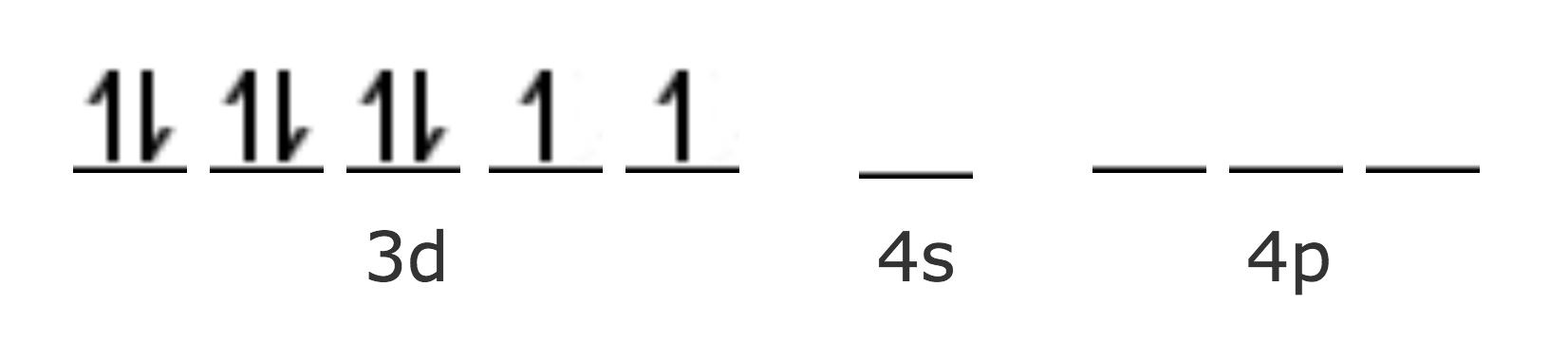
Para los complejos con número de coordinación 2 corresponde una hibridación sp, lineal, y para los de número de coordinación 5 puede corresponder una hibridación sp3d, con estructura de bipirámide trigonal.
La explicación de la estructura de los complejos de Cu (II), un ión d9, es una de las limitaciones de la teoría.
| Cu Z=29 [Ar] | 4s1 3d10 |
| Cu2+ [Ar] | 3d9 |
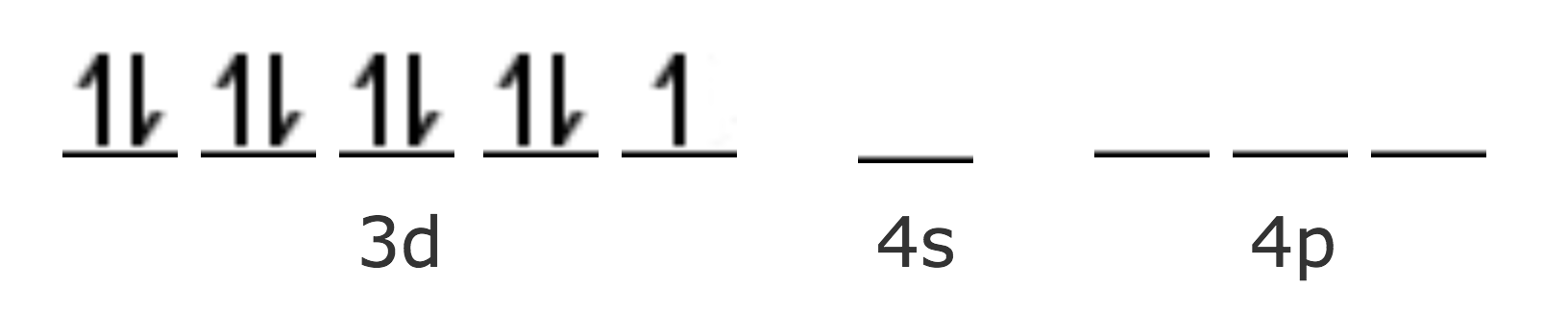
No hay disponible ningún orbital 3d para la hibridación, por lo que sería más fácil sugerir una estructura tetraédrica. Sin embargo, Paulinig sugiere que de acuerdo con los cálculos realizados, la fuerza del enlace es mayor en la hibridación dsp2 que en la sp3. En este caso, este es el factor determinante de la estructura, a pesar de que es necesario que un electrón sufra una transición a un orbital 4p, en la que no se pierde demasiada energía.
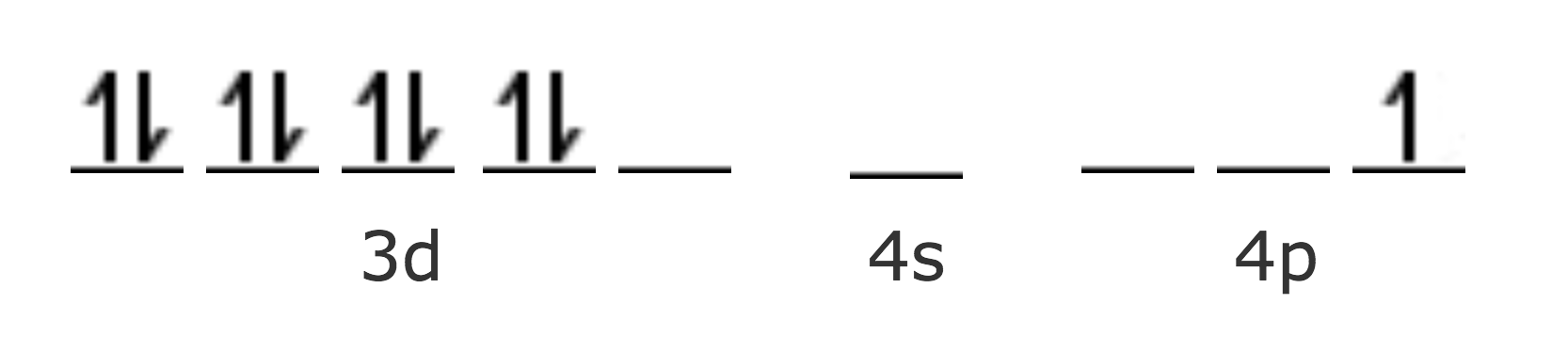
Sin embargo, esto sugeriría una mayor estabilidad de los complejos de Cu (III), los cuales son muy escasos en la naturaleza; esta es otra de las debilidades de la teoría del Enlace Valencia.
El principio de electroneutralidad y el enlace por retrodonación
Una dificultad aparente con la Teoría de Enlace Valencia consiste en que la donación de electrones de la base de Lewis (ligante) al ácido de Lewis (ion metálico) origina una carga negativa formal en el metal. Pauling dio dos razones por las cuales los metales no tienen en realidad tal carga negativa, que son valederas para las diferentes teorías que explican el enlace de coordinación:
- Principio de electroneutralidad: Como los átomos donores de los ligantes son en general altamente electronegativos, los electrones no están igualmente compartidos entre el metal y los ligantes, lo cual induce cargas positivas en el metal que contrarrestan la carga formal negativa. Pauling sugirió que los complejos serían más estables cuando el metal adquiera una condición esencialmente neutra.
- Enlace por retrodonación: El metal aumenta su densidad electrónica por la formación del enlace con los ligantes, tiende a disminuirla devolviendo parte de esta densidad electrónica al ligante por una vía diferente a la primera. El enlace por retrodonación se ilustra en la siguiente figura.
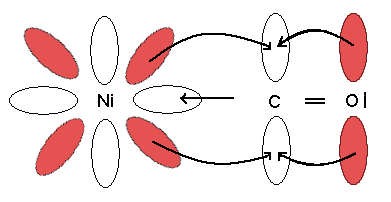
El ión metálico recibe densidad electrónica a través de la formación de enlaces con el ligante, pero tiende a deslocalizarla a través de la superposición de algunos de sus orbitales d con orbitales del ligante. En la TEV, habría una orbital p del carbono que estaría en capacidad de recibir esta densidad electrónica; esta deslocalización electrónica hace que aumente el orden de enlace entre el níquel y el carbono, mientras que disminuye entre el carbono y el oxígeno.
El enlace por retrodonación ha podido comprobarse experimentalmente: el enlace Ni C debería tener una longitud de ~2,16 Å, pero los datos experimentales indican que es de 1,82 Å. Esta distancia tan corta sugiere un carácter de enlace múltiple. Por otra parte, la frecuencia de vibración del CO en el IR es de 2143 cm-1, mientras que en el complejo es de 2060 cm-1. Este desplazamiento a menor frecuencia indica una disminución en el orden de enlace.