SEDE BOGOTA

espacios vectoriales

Lección 6.

Ejercicios

Problema 1. En el conjunto 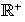$\QTR{Bbb}{R}^{+}$ de números reales positivos se definen las siguientes operaciones:

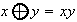
$x\bigoplus y=xy$

(el producto corresponde a la multiplicación corriente de números reales positivos)

$a.x=x^{a}$

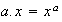
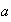( es un número real arbitrario y )

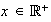Investigar si 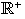$\QTR{Bbb}{R}^{+}$ es un espacio vectorial sobre el cuerpo de números reales.

Solución. Si es un espacio vectorial pues se satisfacen todas las propiedades necesarias para ello. Veamos en detalle cada una de ellas. Sean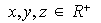 $\;x,y,z\in R^{+}\;$ y $a,b\in R$ , se tiene:

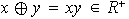
ii)

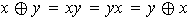
iii)

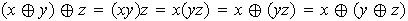
iv)

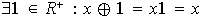
vi) $a.x=x^{a}\in R^{+}$

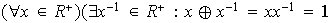
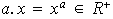
vii)

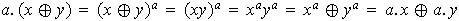
viii)

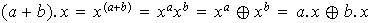
ix)

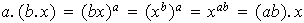
x) $1.x=x^{1}=x$