SEDE BOGOTA

espacios vectoriales

Lección 6.

Ejercicios

Problema 14. Sea 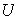el subespacio de $\U{211d} _{3}[x]$ generado por los polinomios 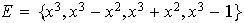. Encontrar un subconjunto 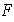de 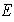linealmente independiente tal que .

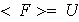Solución.

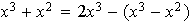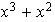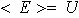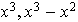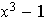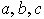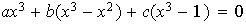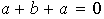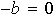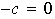Nótese que , luego el elemento $x^{3}+x^{2}$ sobra como generador en . Los tres elementos $x^{3},x^{3}-x^{2}$ y $x^{3}-1$ son linealmente independientes: en efecto, sean escalares reales tales que , entonces , y , o sea que todos los escalares son nulos.