espacios vectoriales
| Lección 6. |
Ejercicios
|
Problema 15. Encontrar una base para el
subespacio
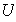de
![$\U{211d} _{4}[x]$](graphics/cap1problema15__2.png)
generado por los polinomios
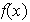que satisfacen la condición
.
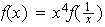Solución.
Sea
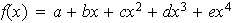tal que
.
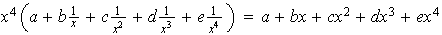Entonces,
,
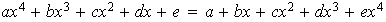es decir,
,
es decir, los polinomios que cumplen la condición son de la forma
.
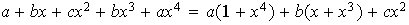Esto dice que los polinomios
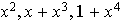generan
.
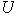Además, estos polinomios son LI, luego forman una base de
.
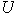