| Lección 6. |
Ejercicios
|
Problema 17. Sea
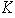 un cuerpo finito con
un cuerpo finito con
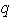 elementos. ¿Cuántas bases ordenadas distintas tiene
elementos. ¿Cuántas bases ordenadas distintas tiene
 ,
,
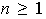 .
.
Solución.
Cualquier base de
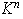 consta de
consta de
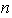 elementos LI. Por tanto, el problema se reduce a construir todos los posibles
conjuntos distintos de
elementos LI. Por tanto, el problema se reduce a construir todos los posibles
conjuntos distintos de
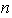 elementos LI en el
espacio
elementos LI en el
espacio 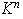 .
Sea
.
Sea
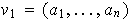 el primer vector de la lista, entonces
el primer vector de la lista, entonces
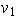 puede ser cualquier vector no nulo, es decir, el número de posibilidades
para
puede ser cualquier vector no nulo, es decir, el número de posibilidades
para
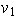 es
es
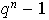 .
El segundo vector de la lista no puede ser múltiplo de
.
El segundo vector de la lista no puede ser múltiplo de
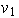 ,
es decir,
,
es decir,
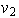 no puede ser de la forma
no puede ser de la forma
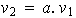 ,
donde
,
donde
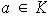 .
Por tanto, el número de posibilidades para
.
Por tanto, el número de posibilidades para
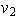 es
es
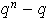 .
Así pues, el número posible de dos vectores LI en
.
Así pues, el número posible de dos vectores LI en
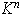 es
es
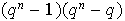 .
Para el tercer vector se debe tener que no puede ser combinación lineal
de los dos anteriores, es decir,
.
Para el tercer vector se debe tener que no puede ser combinación lineal
de los dos anteriores, es decir,
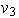 no puede ser de la forma
no puede ser de la forma
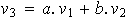 .
Por tanto, el número de posiblidades para
.
Por tanto, el número de posiblidades para
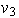 es
es
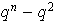 .
Continuando el razonamiento de esta manera se encuentra que el número
total de
.
Continuando el razonamiento de esta manera se encuentra que el número
total de
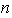 vectores LI es
vectores LI es
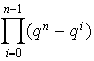 .
.