espacios vectoriales
| Lección 6. |
Ejercicios
|
Problema 3. Sean
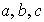números reales diferentes fijos. Investigar si los polinomios
,
,
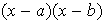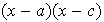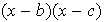son linealmente independientes.
Solución. Consideremos la combinación lineal
.
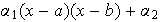
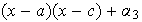
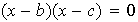Esta relación dice que el polinomio de la izquierda es nulo, luego en
cada valor de
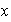este polinomio es cero. Entonces, tomando
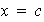y teniendo en cuenta que los valores
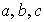son diferentes, se tiene que
.
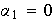De igaul forma se prueba que
.
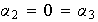