| Lección 4. |
Bases.
|
Proposición 4. Sea
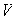un
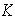-espacio
y
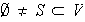. Entonces
(a)
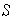es L D si y solo si existe
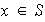tal que
,
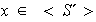donde
.
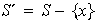(b) Si
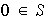entonces
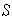es L D.
(c) Si
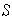es L I entonces cada subconjunto de
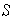es L I.
(d) Si
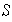es finito con
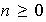elementos, entonces cada conjunto de
elementos de
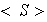es L D.
Demostración. Las afirmaciones (a)-(c) son evidentes. La prueba de la
parte (d) se hace por inducción sobre
.
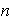El caso
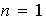es evidente. Supóngase que la afirmación ha sido demostrada para
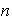vectores pertenecientes a la envolvente lineal de
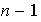vectores LI. Sea
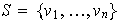un conjunto LI de vectores, y sean
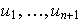vectores de
.
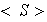Supóngase que estos vectores son LI, y al expresar cada uno de ellos como
combinación lineal de los
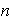vectores de
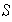se tiene que:
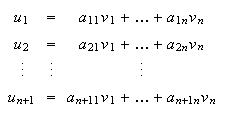
Puesto que los vectores
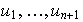son LI, entoces cada uno de ellos es no nulo, en particular
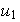es no nulo, esto hace que sin perder generalidad podamos suponer que
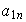es no nulo. Nótese que entonces el siguiente sistema de vectores es LI:
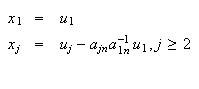
Según la parte (c) los vectores
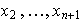son LI, pero al reemplazar
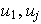en la expresión que define a
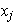se encuentra que estos vectores pertenecen a la envolvente lineal de
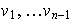y por inducción resultarían
LD.