| Lección 5. |
DimensiÓn
|
Proposición 8. Sea
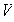un espacio vectorial con bases infinitas
.
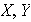Entonces
.
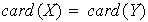Demostración. La idea es probar que
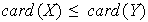y utilizar la simetría del problema para
concluir que
.
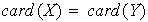Cada elemento
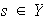es representable mediante una combinación lineal finita de elementos de
.
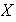Además, dado
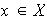existe
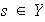tal que
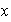se encuentra en la representación de
.
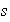En efecto, sea
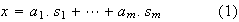
la representación de
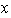en términos de elementos de
.
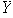Cada elemento
,
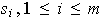es representable como combinación lineal de elementos de
;
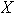si se supone que
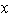no aparece en la representación de ningún elemento de
,
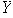entonces
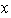no aparece en la representación de ninguno de los elementos
.
Sea
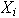el conjunto (finito !) de elementos de
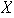que intervienen en la representación de
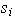y sea
.
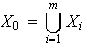Obviamente
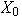es finito y
.
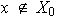De (1) se obtiene que
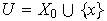es L D, pero esto contradice el hecho de que
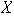es una base.
Así pues, dado
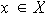existe al menos un
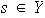tal que
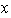está en la representación de
.
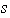Usando el axioma de elección se define la función
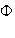
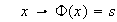
donde
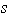es un elemento de
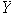tal que
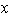está en la representación de
.
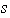Sea
,
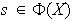entonces
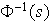es un conjunto (finito !) y consta de elementos de
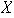que intervienen en la representación de
.
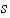Se establece, de esta manera, una función entre
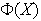y el conjunto
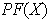de partes finitas de
:
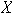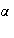
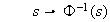
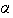es inyectiva ya que
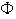es una función ; por tanto
.
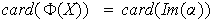Enseguida se probará que
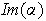es una partición de
.
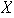Si
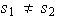son dos elementos de
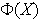entonces
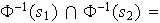
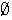debido a que
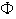es una función. Claramente
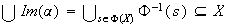
Sea
,
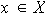entonces
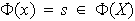con lo cual
,
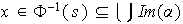es decir,
.
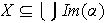Puesto que
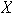es infinito
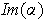también es infinito. Así, se tiene que
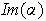es una partición infinita de partes finitas de
,
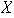con lo cual
.
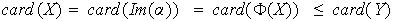Esto completa la prueba de la
proposición.