| Lección 1. |
Estructuras Algebraicas BÁsicas.
|
Sea
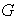 un conjunto no vacío. Una operación
binaria interna en
un conjunto no vacío. Una operación
binaria interna en
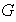 es una función
es una función
 con dominio
con dominio
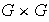 y codominio
y codominio
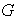 :
:
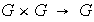
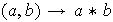
Si la operación
 es asociativa en el sentido que
es asociativa en el sentido que
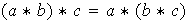
para cualesquiera elementos
,
entonces se dice que
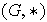 es un semigrupo.
es un semigrupo.
Ejemplo 1. El
conjunto
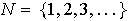 de números naturales con la operación usual de adición es un
semigrupo.
de números naturales con la operación usual de adición es un
semigrupo.
Si en el semigrupo
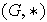 existe un elemento
existe un elemento
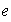 tal que
tal que
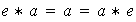
para cada elemento
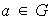 ,
entonces se dice que
,
entonces se dice que
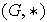 es un monoide con
elemento neutro
es un monoide con
elemento neutro
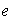 .
.
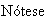 que en un monoide el elemento neutro es único.
que en un monoide el elemento neutro es único.
Ejemplo 2. El conjunto
 de números enteros con la operación usual de multiplicación es
un monoide con elemento neutro
de números enteros con la operación usual de multiplicación es
un monoide con elemento neutro
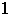 .
.
Sea
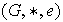 un monoide. Si cada elemento
un monoide. Si cada elemento
 tiene un inverso , es decir, existe un elemento
tiene un inverso , es decir, existe un elemento
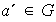 tal que
tal que
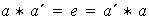
entonces se dice que
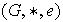 es un grupo. Nótese que en un grupo cada
elemento tiene un único inverso. Si el contexto lo permite, un grupo
es un grupo. Nótese que en un grupo cada
elemento tiene un único inverso. Si el contexto lo permite, un grupo
 será denotado simplemente por
será denotado simplemente por
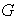 .
.
Ejemplo 3. El conjunto
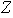 de números enteros con la operación usual de adición conforma
un grupo.
de números enteros con la operación usual de adición conforma
un grupo.
Un grupo
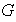 se dice
conmutativo ( = abeliano)
si su op
se dice
conmutativo ( = abeliano)
si su op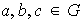 eración es conmutativa,
es decir,
eración es conmutativa,
es decir,
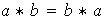
para cualesquiera elementos
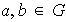 .
Obsérvese que el grupo aditivo de números enteros es conmutativo. Se
acostumbra a denotar la operación de un grupo conmutativo mediante el
símbolo
.
Obsérvese que el grupo aditivo de números enteros es conmutativo. Se
acostumbra a denotar la operación de un grupo conmutativo mediante el
símbolo
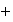 .
.
Se ha visto que el conjunto
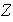 de números enteros posee dos operaciones
de números enteros posee dos operaciones
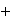 y
y
 tal que respecto de la primera es un grupo abeliano, mientras que bajo la
segunda es un monoide. Conjuntos con tales condiciones conforman los llamados
anillos. Más exactamente, un
anillo es un conjunto
tal que respecto de la primera es un grupo abeliano, mientras que bajo la
segunda es un monoide. Conjuntos con tales condiciones conforman los llamados
anillos. Más exactamente, un
anillo es un conjunto
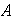 dotado de dos operaciones
dotado de dos operaciones
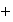 y
y
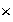 tales que:
tales que:
(a)
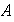 respecto de
respecto de
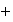 es un grupo conmutativo
es un grupo conmutativo
(b)
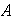 respecto de
respecto de
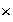 es un monoide
es un monoide
(c)
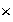 se distribuye sobre
se distribuye sobre
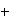 ,
es decir,
,
es decir,
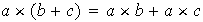
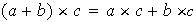
para cualesquiera elementos
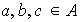 .
El anillo
.
El anillo
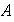 es conmutativo si su segunda operación es
conmutativa.
es conmutativo si su segunda operación es
conmutativa.
En adelante
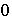 denotará el elemento neutro de la primera operación en
denotará el elemento neutro de la primera operación en
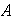 ,
,
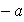 será el inverso de
será el inverso de
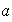 respecto de dicha operación y lo llamaremos el
opuesto de
respecto de dicha operación y lo llamaremos el
opuesto de
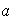 ;
;
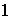 denotará el elemento neutro de
denotará el elemento neutro de
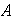 respecto de la segunda operación y lo llamaremos el
uno de
respecto de la segunda operación y lo llamaremos el
uno de
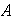 .
Además, es costumbre omitir el
.
Además, es costumbre omitir el
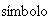
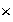 entre dos elementos, así pues, el producto
entre dos elementos, así pues, el producto
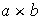 se escribirá simplemente como
se escribirá simplemente como
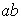 .
.
Ejemplo 4. El conjunto
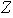 de números enteros con las operaciones habituales de adición y
multiplicación es un anillo conmutativo.
de números enteros con las operaciones habituales de adición y
multiplicación es un anillo conmutativo.
Ejemplo 5. El conjunto
![$\QTR{large}{R[x]}$](graphics/cap1s1__63.png) de polinomios reales en la indeterminada
de polinomios reales en la indeterminada
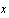 con
las operaciones habituales de adición y multiplicación de polinomios
es un anillo conmutativo.
con
las operaciones habituales de adición y multiplicación de polinomios
es un anillo conmutativo.
Ejemplo 6. El conjunto
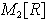 de matrices reales
de matrices reales
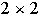 con
las operaciones usuales de adición y multiplicación de matrices
conforma un anillo.
con
las operaciones usuales de adición y multiplicación de matrices
conforma un anillo.
En un anillo
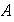 cada elemento
cada elemento
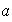 tiene un opuesto
tiene un opuesto
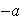 ,
sin embargo, no todo elemento tiene un inverso respecto de la segunda
operación. Por ejemplo, en
,
sin embargo, no todo elemento tiene un inverso respecto de la segunda
operación. Por ejemplo, en
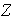 el 2 no tiene inverso multiplicativo, es decir, no existe entero
el 2 no tiene inverso multiplicativo, es decir, no existe entero
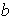 tal que
tal que
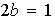 .
En
.
En
![$\QTR{large}{R[x]}$](graphics/cap1s1__73.png) los únicos polinomios invertibles son las constantes no nulas; en
los únicos polinomios invertibles son las constantes no nulas; en
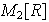 las matrices de determinante no nulo son invertibles.
las matrices de determinante no nulo son invertibles.
Si
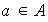 es invertible, entonces existe un único
es invertible, entonces existe un único
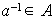 tal que
tal que
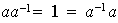 ; la colección de elementos invertibles de
; la colección de elementos invertibles de
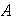 se denota por
se denota por
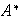 .
.
Ejemplo 7.
(a)
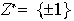
(b)
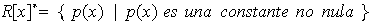
(c)
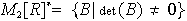 .
.
Proposición 1.
Si
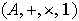 es un anillo, entonces
es un anillo, entonces
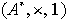 es un grupo.
es un grupo.
Un anillo conmutativo
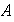 es un cuerpo si cada
elemento no nulo de
es un cuerpo si cada
elemento no nulo de
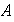 tiene inverso multiplicativo. En otras palabras,
tiene inverso multiplicativo. En otras palabras,
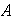 es un cuerpo si
es un cuerpo si
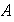 es conmutativo y
es conmutativo y
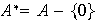 .
.
Ejemplo 8. El conjunto
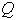 de números racionales con las operaciones usuales de adición y
multiplicación es un cuerpo. De igual manera, los conjuntos
de números racionales con las operaciones usuales de adición y
multiplicación es un cuerpo. De igual manera, los conjuntos
 y
y
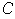 de números reales y complejos, respectivamente, con las operaciones
usuales de adición y multiplicación son ejemplos de cuerpos.
de números reales y complejos, respectivamente, con las operaciones
usuales de adición y multiplicación son ejemplos de cuerpos.
Esta sección se cierra con el concepto de
isomorfismo, el cual permite clasificar los diferentes tipos de estructuras
(grupos, anillos, cuerpos, etc...) de acuerdo a que sean
"iguales" desde el punto de vista algebraico. La
importancia de este concepto se entenderá más adelante; por ahora
presentamos la definición. Dos grupos
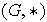 y
y
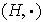 se dicen isomorfos si existe una función
biyectiva
se dicen isomorfos si existe una función
biyectiva
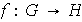
tal que
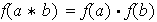
para cualesquiera elementos
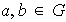 .
Dos anillos
.
Dos anillos
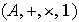 y
y
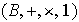 se dicen isomorfos si existe una función biyectiva
se dicen isomorfos si existe una función biyectiva
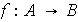
tal que
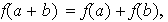
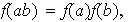
para cualesquiera elementos
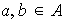 .
Obsérvese que necesariamente
.
Obsérvese que necesariamente
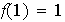 y
y
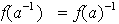 para cada elemento invertible de
para cada elemento invertible de
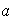 de
de
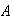 .
Además, la relación "ser isomorfo" es de
equivalencia.
.
Además, la relación "ser isomorfo" es de
equivalencia.