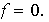formas bilineales
| Lección 5. |
Formas Sesquilineales
|
Teorema 4. Sea
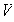un espacio real o complejo de dimensión finita 
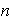y sea
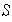el espacio de formas sesquilineales sobre
.
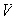Entonces,
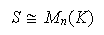
con
.
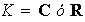En consecuencia,
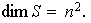
Demostración. Fijemos una base ordenada cualquiera
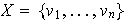en
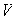y consideremos la función
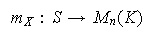
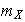es claramente
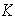-lineal.
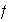puede escribirse matricialmente con ayuda de
,
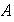en la siguiente forma: sean
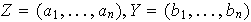las coordenadas de
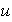y
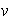respectivamente en la base X. Entonces,
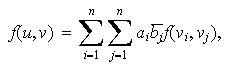
es sobreyectiva: sea
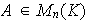y
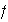definida como en (3). Entonces,
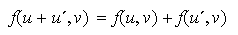
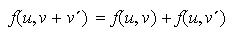
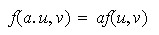
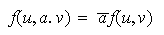
y además
.
Finalmente nótese que
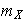es inyectiva: si
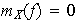entonces, según (3),
,
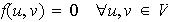es decir,
