| Lección 1. |
Leyes de Composición - Definición y Ejemplos
|
En esta sección definimos el concepto de operación entre elementos de un conjunto; concepto que hemos utilizado tácitamente en todas nuestras matemáticas elementales. Se dará además una definición precisa de las propiedades más comunes de las que gozan estas operaciones. Esto permitirá introducir posteriormente la noción de grupo.
Definición 1. Sea
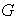 un conjunto no vacío. Cualquier función
un conjunto no vacío. Cualquier función
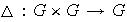 del producto cartesiano de
del producto cartesiano de
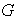 por
por
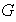 en el mismo conjunto
en el mismo conjunto
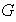 se denomina ley de composición interna definida en el conjunto
se denomina ley de composición interna definida en el conjunto
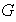 .
Así pues, a cada par ordenado
.
Así pues, a cada par ordenado
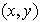 de elementos de
de elementos de
 se le asigna un único elemento de
se le asigna un único elemento de
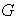 .
La imágen del par
.
La imágen del par
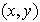 mediante la función
mediante la función
 se denota por
se denota por
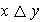 .
.
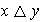 se denomina también resultado de operar
se denomina también resultado de operar
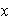 e
e
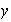 (en ese orden).
(en ese orden).
Ejemplo 1. La adición de números naturales es una ley de composición :
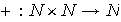
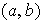 \
\ 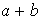
Ejemplo 2. En
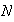 podemos definir la función
podemos definir la función
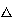 como sigue:
como sigue:
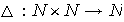
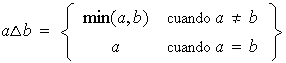
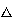 es una ley de composición interna en
es una ley de composición interna en
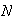 .
Por ejemplo,
3
.
Por ejemplo,
3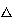 4=3
, 5
4=3
, 5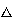 2=2,
3
2=2,
3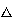 3=3.
3=3.
Ejemplo 3. Sea
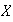 un conjunto finito y sea
un conjunto finito y sea
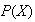 el conjunto de todos los subconjuntos de
el conjunto de todos los subconjuntos de
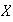 .
La intersección de conjuntos define una operación binaria interna en
.
La intersección de conjuntos define una operación binaria interna en
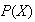 :
:
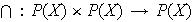
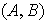 \
\ 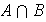
Ejemplo 4. En el conjunto
de los números naturales
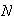 definamos la función:
definamos la función:
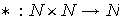
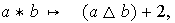
donde la operación
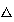 es como en el Ejemplo 2.
es como en el Ejemplo 2.
Así pues,
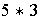 =
(5
=
(5 3)
+ 2 = 3 + 2 =5
3)
+ 2 = 3 + 2 =5
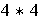 =
(4
=
(4 4)
+ 2 = 4 + 2 = 6
4)
+ 2 = 4 + 2 = 6
Ejemplo 5. La función
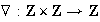 ,
dada por
,
dada por
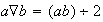 , no define en
, no define en
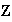 una operación binaria interna.
una operación binaria interna.
Dado un conjunto
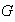 con una operación binaria interna
con una operación binaria interna
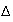 y dados 3 elementos
y dados 3 elementos
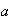 ,
,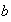 y
y
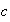 del conjunto
del conjunto
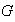 ,
podemos preguntarnos las maneras de operar estos tres elementos en ese orden e
investigar si los resultados de estas formas de operar coinciden. Así
pues, en el Ejemplo 1 sean 2,5, 7
,
podemos preguntarnos las maneras de operar estos tres elementos en ese orden e
investigar si los resultados de estas formas de operar coinciden. Así
pues, en el Ejemplo 1 sean 2,5, 7
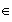 N.
N.
Entonces 2+5=7 7+7=14
5+7=12 2+12=14
Es decir, (2+5) +7 = 2+(5+7), donde los paréntesis indican la secuencia en que se han efectuado las operaciones.
Es bien conocido que para la adición de números naturales esta
propiedad es válida, es decir que cualesquiera que sean
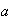 ,
,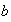 ,
,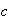
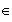
 , se cumple que
, se cumple que
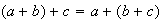 .
Nótese sin embargo en el Ejemplo 4, que sobre el mismo conjunto
.
Nótese sin embargo en el Ejemplo 4, que sobre el mismo conjunto
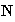 se definió la operación
se definió la operación
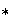 que no cumple esta propiedad:
que no cumple esta propiedad:
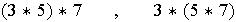

7
 5
5
Esto permite clasificar las operaciones binarias de acuerdo a esta propiedad o condición.
Definición 2.
Sea
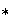 una operación binaria definida sobre un conjunto
una operación binaria definida sobre un conjunto
 .
Se dice que la operación
.
Se dice que la operación
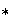 tiene la propiedad asociativa, o que * es una operación asociativa, si
para cualesquiera elementos
tiene la propiedad asociativa, o que * es una operación asociativa, si
para cualesquiera elementos
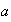 ,
,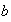 ,
,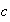 de
de
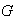 se cumple la igualdad
se cumple la igualdad
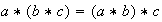 .
.
De esta definición surge una pregunta inmediata: En el caso de que sean
dados 4, 5, ó
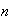 elementos (en un orden determinado) la secuencia en que se efectuen las
operaciones influye en el resultado? Se puede probar que si la operación
es asociativa, es decir si para el caso de 3 elementos se tiene la propiedad
exigida, entonces la misma propiedad tendrá lugar para cualesquiera
elementos (en un orden determinado) la secuencia en que se efectuen las
operaciones influye en el resultado? Se puede probar que si la operación
es asociativa, es decir si para el caso de 3 elementos se tiene la propiedad
exigida, entonces la misma propiedad tendrá lugar para cualesquiera
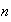 elementos dados en un orden determinado, es decir, que si se dan
elementos dados en un orden determinado, es decir, que si se dan
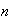 elementos
elementos
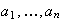 del conjunto
del conjunto
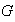 y suponiendo que la operación
y suponiendo que la operación
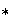 de
de
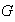 es asociativa, los paréntesis que indican la secuencia de como se
realizan las operaciones en la expresión
es asociativa, los paréntesis que indican la secuencia de como se
realizan las operaciones en la expresión
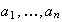 pueden ser colocados donde se quiera y el resultado no varía.
pueden ser colocados donde se quiera y el resultado no varía.