| Lección 2. |
Leyes de Composición - Propiedades y Estructuras Elementales
|
Proposición 1. Sea
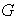 un conjunto donde se ha definido una operación binaria asociativa
un conjunto donde se ha definido una operación binaria asociativa
 .
Sea
.
Sea
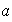 cualquier elemento de
cualquier elemento de
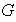 .
Se define
.
Se define
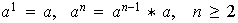 .
.
Entonces, para cualesquiera naturales
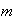 y
y
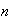 se tienen las identidades
se tienen las identidades
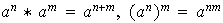
Definición 3. Un
semigrupo es un conjunto
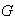 dotado de una operación binaria interna asociativa
dotado de una operación binaria interna asociativa
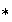 .
En este caso se dice también que sobre
.
En este caso se dice también que sobre
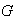 se tiene una estructura de semigrupo. Algunas veces se acostumbra denotar al
semigrupo
se tiene una estructura de semigrupo. Algunas veces se acostumbra denotar al
semigrupo
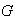 acompañado de la operación asociativa
acompañado de la operación asociativa
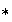 :
:
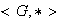 .
.
Ejemplo 6.
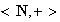 es un semigrupo.
es un semigrupo.
Ejemplo 7. Sea
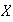 un conjunto no vacío cualquiera y sea
un conjunto no vacío cualquiera y sea
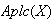 el conjunto de aplicaciones (funciones) de
el conjunto de aplicaciones (funciones) de
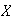 en si mismo. Por teoría elemental de conjuntos sabemos que la
operación composición de funciones
en si mismo. Por teoría elemental de conjuntos sabemos que la
operación composición de funciones
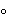 es una operación binaria interna en
es una operación binaria interna en
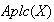 y además es asociativa. Así pues,
y además es asociativa. Así pues,
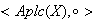 es un semigrupo.
es un semigrupo.
En el análisis de la propiedad asociativa exigiamos la condición de
no cambiar el orden en que fueran dados los elementos. Este hecho es
fundamental ya que no toda operación binaria
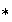 definida sobre un conjunto
definida sobre un conjunto
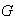 cumple que
cumple que
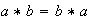 para todos los elementos
para todos los elementos
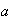 y
y
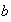 de
de
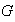 .
.
Definición 4. Sea
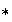 una operación binaria definida sobre un conjunto
una operación binaria definida sobre un conjunto
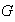 .
Se dice que la operación
.
Se dice que la operación
 es conmutativa si para cualesquiera elementos
es conmutativa si para cualesquiera elementos
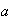 y
y
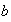 de
de
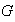 se tiene que:
se tiene que:
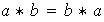 .
.
Proposición 2. Sea
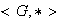 un semigrupo conmutativo, es decir, la operación binaria
un semigrupo conmutativo, es decir, la operación binaria
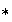 es asociativa y conmutativa. Entonces, para cualequiera
es asociativa y conmutativa. Entonces, para cualequiera
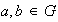 y cualquier natural
y cualquier natural
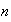 se tiene que:
se tiene que:
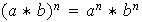 .
.
Existen conjuntos con operaciones binarias internas donde se destacan elementos especiales.
Definición 5.
Sea
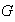 un conjunto en el cual se ha definido una operación binaria
un conjunto en el cual se ha definido una operación binaria
 .
Se dice que el elemento
.
Se dice que el elemento
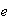 de
de
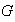 es una identidad de
es una identidad de
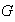 con respecto de la operación
con respecto de la operación
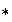 si para cualquier elemento de
si para cualquier elemento de
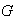 se tiene:
se tiene:
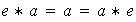
Ejemplo 8.
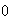 es una identidad del semigrupo
es una identidad del semigrupo
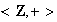 ,
donde
,
donde
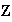 es el conjunto de números enteros.
es el conjunto de números enteros.
Surge la siguiente pregunta: en un conjunto
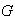 con una operación binaria
con una operación binaria
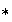 pueden existir varias identidades ?
pueden existir varias identidades ?
Proposición 3. En un
conjunto
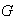 con una operación binaria
con una operación binaria
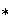 solo puede existir un elemento identidad respecto de la operación
solo puede existir un elemento identidad respecto de la operación
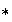 .
.
Nótese que para diferentes operaciones, las identidades no necesariamente
coinciden, como tampoco cada operación debe tener su elemento identidad.
Así pues,
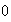 es la identidad del semigrupo
es la identidad del semigrupo
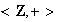 ,
,
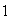 es la identidad de
es la identidad de
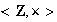 y
y
 no tiene identidad.
no tiene identidad.
Definición 6. Un monoide es un semigrupo que posee elemento identidad.
Definición 7.
Sea
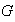 un conjunto dotado de una operación binaria interna
un conjunto dotado de una operación binaria interna
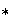 la cual posee un elemento identidad
la cual posee un elemento identidad
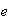 ,
se dice que elemento
,
se dice que elemento
 de
de
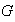 es invertible si existe
es invertible si existe
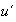 en
en
 tal que
tal que
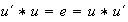 ,
en donde
,
en donde
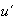 se denomina el inverso de
se denomina el inverso de
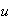 respecto a la operación
respecto a la operación
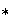 .
.
En la definición anterior no se exige que cada elemento de
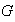 sea invertible. Sin embargo de esta definición se desprende lo siguiente:
sea invertible. Sin embargo de esta definición se desprende lo siguiente:
Proposición 4. Sea
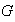 un monoide. Si
un monoide. Si
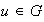 es invertible entonces su inverso
es invertible entonces su inverso
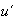 es único.
es único.
Proposición 5. Sea
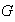 un monoide y sean
un monoide y sean
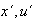 los inversos de
los inversos de
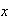 ,
,
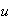 respectivamente. Entonces
respectivamente. Entonces
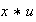 es invertible y
es invertible y
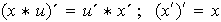 .
.