| Lección 3. |
Leyes de Composición - Ejercicios
|
Ejercicio 1. Demostrar por inducción las proposiciones 1 y 2.
Ejercicio 2. Definición: Sea
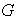 un conjunto dotado de una operación binaria interna
un conjunto dotado de una operación binaria interna
 , se dice que un elemento
, se dice que un elemento
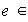 G es:
G es:
(a) Identidad a la izquierda de
 si,
si,
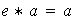 ,
cualquiera que sea
,
cualquiera que sea
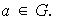
(b) Identidad a la derecha de
 si,
si,
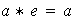 ,
cualquiera que sea
,
cualquiera que sea
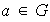 .
.
Sean
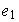 y
y
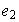 elementos de
elementos de
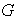 tales que
tales que
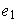 es identidad a la izquierda de
es identidad a la izquierda de
 y
y
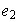 es identidad a la derecha de
es identidad a la derecha de
 ,
probar que
,
probar que
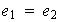 .
.
Ejercicio 3. Comprobar que en
(a)
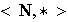 donde
donde
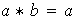 , todo elemento de
, todo elemento de
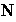 es identidad a la derecha , pero no existe identidad a la izquierda.
es identidad a la derecha , pero no existe identidad a la izquierda.
(b)
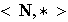 donde
donde
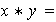 máximo común divisor de
máximo común divisor de
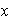 e
e
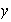 no posee elementos identidad.
no posee elementos identidad.
(c)
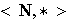 donde
donde
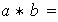 mínimo común múltiplo de
mínimo común múltiplo de
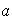 y
y
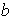 ,
,
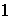 es el elemento identidad.
es el elemento identidad.
(d)
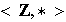 donde
donde
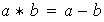 ,
,
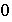 es identidad a la derecha pero no posee identidad a la izquierda.
es identidad a la derecha pero no posee identidad a la izquierda.
Ejercicio 4. Encontrar en el semigrupo
 el elemento identidad.
el elemento identidad.
Ejercicio 5. Sea
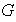 un conjunto dotado de una operación binaria interna
un conjunto dotado de una operación binaria interna
 asociativa, la cual posee elemento identidad
asociativa, la cual posee elemento identidad
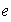 .
Sea
.
Sea
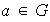 ,
se dice que
,
se dice que
(a)
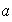 posee un inverso a la izquierda (respecto de
posee un inverso a la izquierda (respecto de
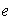 )
si existe
)
si existe
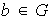 tal que
tal que
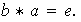
ii)
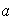 posee un inverso a la derecha ( respecto de
posee un inverso a la derecha ( respecto de
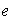 )
si existe
)
si existe
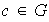 tal que
tal que
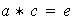 .
.
Demostrar que si
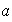 posee un inverso a la izquierda
posee un inverso a la izquierda
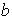 y un inverso a la derecha
y un inverso a la derecha
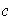 ,
entonces
,
entonces
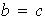 .
A partir de esto deducir la Proposición 4.
.
A partir de esto deducir la Proposición 4.
Ejercicio 6. Determinar en
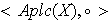 los elementos invertibles.
los elementos invertibles.
Ejercicio 7 Demostrar la Proposición 5.
Ejercicio 8. Sean
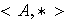 y
y
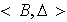 conjuntos con operaciones binarias internas . Una función
conjuntos con operaciones binarias internas . Una función
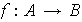 , del conjunto
, del conjunto
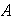 en el conjunto
en el conjunto
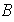 se denomina un homomorfismo si
se denomina un homomorfismo si
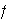 respeta las operaciones de los conjuntos
respeta las operaciones de los conjuntos
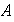 y
y
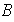 ,
es decir,
,
es decir,
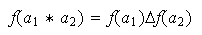
para cualesquiera elementos
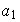 ,
,
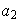 de
de
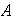 .
Además, si
.
Además, si
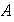 y
y
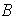 poseen elementos identidad
poseen elementos identidad
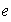 y
y
 respectivamente, entonces
respectivamente, entonces
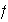 debe cumplir la propiedad adicional
debe cumplir la propiedad adicional
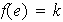 .
.
Sea
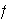 un homomorfismo de
un homomorfismo de
 en
en
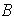 .
Probar por inducción que
.
Probar por inducción que
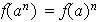 para todo
para todo
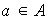 y todo
y todo
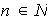 .
Probar además que si
.
Probar además que si
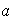 es invertible en
es invertible en
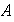 ,
entones
,
entones
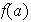 es invertible en
es invertible en
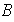 ,
cumpliéndose la fórmula
,
cumpliéndose la fórmula
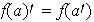 .
.
Ejercicio 9. Sea
 un homomorfismo de
un homomorfismo de
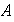 en
en
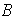 ,
donde
,
donde
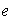 y
y
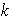 son los respectivos elementos identidad. Se definen los siguientes objetos:
son los respectivos elementos identidad. Se definen los siguientes objetos:
(a) El conjuntode imágenes de la función
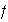 se llama imágen del homomorfismo
se llama imágen del homomorfismo
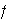 y se simboliza por
y se simboliza por
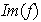 ,
así pues
,
así pues
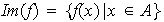
(b) El conjunto de elementos de
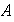 cuya imagen es el elemento identidad
cuya imagen es el elemento identidad
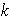 se llama el núcleo del homomorfismo
se llama el núcleo del homomorfismo
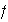 y se simpoliza por
y se simpoliza por
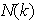 o también
o también
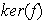 (de la palabra alemana Kernel). Así pues,
(de la palabra alemana Kernel). Así pues,
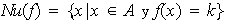
(c) Se dice que
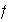 es un sobreyectivo si la función
es un sobreyectivo si la función
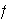 es sobreyectiva, es decir,
es sobreyectiva, es decir,
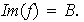
(d) Se dice que el homomorfismo
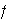 es inyectivo si la función
es inyectivo si la función
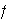 es inyectiva, es decir, para cualesquiera elementos
es inyectiva, es decir, para cualesquiera elementos
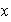 ,
,
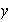 en
en
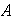 la igualdad
la igualdad
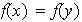 implica
implica
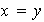 .
.
(e) Se dice que
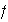 es un isomorfismo si
es un isomorfismo si
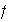 es sobreyectivo e inyectivo.
es sobreyectivo e inyectivo.
(f) Si los conjuntos
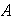 y
y
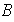 coinciden y las operaciones
coinciden y las operaciones
 ,
y,
,
y,
 también, entonces un isomorfismo
también, entonces un isomorfismo
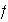 en este caso se denomina automorfismo de
en este caso se denomina automorfismo de
 .
.
Sea
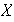 un conjunto y sea
un conjunto y sea
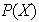 su conjunto de partes. Sea
su conjunto de partes. Sea
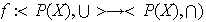 la función que a cada subconjunto
la función que a cada subconjunto
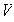 de
de
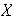 le asigna su complemento:
le asigna su complemento:
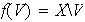 .
.
Determinar las identidades en
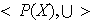 y
y
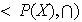 y comprobar que
y comprobar que
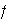 es un isomorfismo. Es
es un isomorfismo. Es
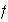 un automorfismo de
un automorfismo de
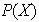 ?
?
(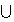 representa la unión de conujuntos , así como
representa la unión de conujuntos , así como
 representa la intersección).
representa la intersección).
Ejercicio 10. Sea
 un conjunto dotado de una ley de composición interna
un conjunto dotado de una ley de composición interna
 .
Supóngase que en
.
Supóngase que en
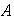 ha sido definida una relación de equivalencia
ha sido definida una relación de equivalencia
 Se dice que la relación
Se dice que la relación
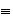 es compatible con la operación
es compatible con la operación
 si para cualesquiera
si para cualesquiera
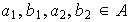 ,
,
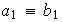 y
y
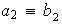 ,
implica
,
implica
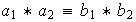 .
Denotemos para
.
Denotemos para
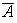 el conjunto
el conjunto
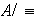 de clases de equivalencia
de clases de equivalencia
![$[a],a\in A$](graphics/cap1s1c__138.png) .
Se desea definir en
.
Se desea definir en
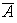 una operación binaria inducida por
una operación binaria inducida por
 y
y
 :
sean [a] y [b] elementos de
:
sean [a] y [b] elementos de
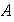 entonces colocamos
entonces colocamos
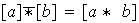 (1).
(1).
(a) Demostrar que (1) define una operación binaria en
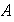 ,
es decir , comprobar que para otros representantes
,
es decir , comprobar que para otros representantes
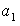 y
y
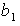 de las clases
de las clases
![$[a]$](graphics/cap1s1c__147.png) y
y
![$[b]$](graphics/cap1s1c__148.png) respectivamente, se cumple que
respectivamente, se cumple que
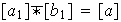 \overline
\
\overline
\![$[b]$](graphics/cap1s1c__150.png) .
.
(b) La función
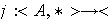 \overline
A,
\overline
A,
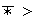 que asigna a cada elemento
que asigna a cada elemento
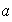 de
de
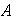 su clase
su clase
![$[a]$](graphics/cap1s1c__155.png) es un homomorfismo sobreyectivo.
es un homomorfismo sobreyectivo.
Ejercicio 11. Sea
 un homomorfismo sobreyectivo. Definimos en
un homomorfismo sobreyectivo. Definimos en
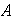 la relación
la relación
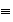 como sigue:
como sigue:
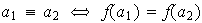 ,
para cualesquiera
,
para cualesquiera
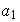 ,
,
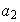 en
en
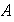 .
.
(a) Demostrar que
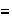 es una relación de equivalencia.
es una relación de equivalencia.
(b) Demostrar que
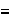 es compatible con
es compatible con
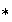 ,
es decir, si
,
es decir, si
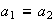 y
y
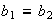 ,
entonces
,
entonces
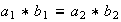 .
.
(c) Sean
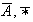 definidos como en el Ejercicio 10. Entonces demostrar que
definidos como en el Ejercicio 10. Entonces demostrar que
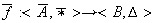 definido por
definido por
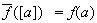 es un isomorfismo.
es un isomorfismo.
(Como toda función definida sobre un conjunto cociente, es importante
probar como primer paso que
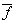 está bien definida, es decir que si
está bien definida, es decir que si
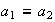 ,
entonces
,
entonces
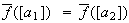 ).
).