| Lección 4. |
Grupos - Concepto
|
En la lección anterior fueron estudiadas algunas propiedades que pueda
tener una operación binaria definida en un conjunto. Así pues, se
dijo que cuando la operación binaria
 definida sobre el conjunto
definida sobre el conjunto
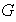 es asociativa se obtiene sobre el conjunto
es asociativa se obtiene sobre el conjunto
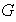 una estructura de semigrupo y se dice entonces que
una estructura de semigrupo y se dice entonces que
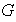 es un semigrupo bajo la operación
es un semigrupo bajo la operación
 .
Al poseer la operación
.
Al poseer la operación
 más propiedades, la estructura se hace más rica y las posibilidades
de operar en
más propiedades, la estructura se hace más rica y las posibilidades
de operar en
 se hacen mayores. Un ejemplo de tal situación lo constituyen los llamados
grupos, los cuales pasamos a definir.
se hacen mayores. Un ejemplo de tal situación lo constituyen los llamados
grupos, los cuales pasamos a definir.
Definición 8. Sea
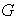 un conjunto no vacío y
un conjunto no vacío y
 una operación binaria definida en
una operación binaria definida en
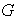 .
Se dice que
.
Se dice que
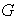 es un grupo respecto de
es un grupo respecto de
 o que
o que
 da a
da a
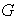 una estructura de grupo si
una estructura de grupo si
 cumple las siguientes propiedades:
cumple las siguientes propiedades:
(a)
 es asociativa
es asociativa
(b) En
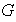 existe un elemento identidad
existe un elemento identidad
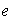 respecto de
respecto de

(c) Cada elemento de
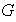 es invertible
es invertible
Para denotar un grupo se utilizará la letra
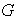 acompañada de la operación
acompañada de la operación
 definida en
definida en
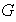 y esto dentro de un paréntesis
y esto dentro de un paréntesis
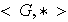 .
Cuando no haya ambiguedad sobre la operación
.
Cuando no haya ambiguedad sobre la operación
 escribiremos simplemente
escribiremos simplemente
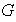 para denotar el grupo.
para denotar el grupo.
Definición 9. Un grupo
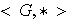 se dice conmutativo o abeliano si la operación
se dice conmutativo o abeliano si la operación
 es conmutativa.
es conmutativa.
Ejemplo 9. Los siguientes conjuntos numéricos con las operaciones indicadas constituyen grupos conmutativos. Además se ha destacado el elemento identidad de cada grupo:
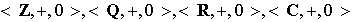
(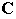 denota el conjunto de números complejos).
denota el conjunto de números complejos).
Ejemplo 10. Los siguientes ejemplos no conforman grupos:
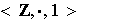 sólo hay dos elementos invertibles:
sólo hay dos elementos invertibles:
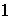 y
y
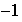
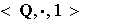 el cero no es invertible
el cero no es invertible
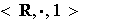 el cero no es invertible
el cero no es invertible
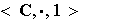 el cero no es invertible.
el cero no es invertible.
Ejemplo 11 El grupo de elementos invertibles de
un semigrupo: Sea
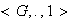 un semigrupo con elemento identidad
un semigrupo con elemento identidad
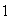 .
Entonces el conjunto de elementos de
.
Entonces el conjunto de elementos de
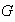 que son invertibles no es vacío y, bajo la misma operación
que son invertibles no es vacío y, bajo la misma operación
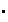 ,
constituye un grupo. Este grupo se simboliza por
,
constituye un grupo. Este grupo se simboliza por
 .
.
Realmente
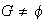 ya que
ya que
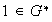 .
Sean
.
Sean
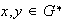 .
Debemos verificar que
.
Debemos verificar que
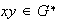 :
:
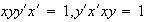 , así que
, así que
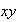 es invertible con inverso
es invertible con inverso
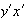 .
Esto prueba que
.
Esto prueba que
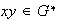 .
.
Puesto que la operación que actúa sobre los elementos de
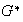 es la misma que la de
es la misma que la de
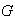 ,
entonces la propiedad asociativa también se cumple para
,
entonces la propiedad asociativa también se cumple para
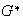 .
.
Ya hemos visto que
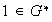 ,
así que en
,
así que en
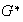 hay elemento identidad. Por último, de acuerdo a nuestra escogencia de
hay elemento identidad. Por último, de acuerdo a nuestra escogencia de
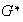 ,
cada uno de sus elementos es invertible respecto de la operación
,
cada uno de sus elementos es invertible respecto de la operación

Nótese por ejemplo que
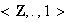 es un semigrupo conmutativo con elemento identidad
es un semigrupo conmutativo con elemento identidad
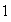 ,
y además
,
y además
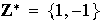 .
.
Por último observemos que
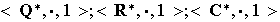
son grupos conmutativos, donde