| Lección 5. |
Grupos - Propiedades Básicas
|
Proposición 6. Sea
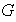 un grupo. Entonces:
un grupo. Entonces:
(a) El elemento identidad
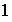 del grupo
del grupo
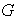 es único
es único
(b) Cada elemento
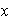 de
de
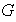 tiene un único inverso
tiene un único inverso

(c) En
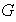 se cumple la ley cancelativa, es decir, que para cualesquiera elementos
se cumple la ley cancelativa, es decir, que para cualesquiera elementos
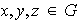 se dan las relaciones
se dan las relaciones

(d) Sean
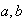 ,
elementos cualesquiera de
,
elementos cualesquiera de
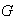 ,
entonces las ecuaciones lineales
,
entonces las ecuaciones lineales
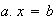 y
y
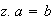 tienen solución única en
tienen solución única en
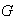 .
.
La proposición que demostraremos a continuación nos indica que los axiomas o propiedades que definen un grupo pueden ser debilitadas.
Proposición 7. Sea
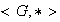 un semigrupo. Entonces
un semigrupo. Entonces
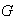 bajo
bajo
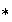 es un grupo si y sólo si
es un grupo si y sólo si
 tiene las siguientes propiedades:
tiene las siguientes propiedades:
(a) Existe un elemento identidad
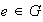 a la izquierada, tal que
a la izquierada, tal que
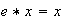 ,
para cada
,
para cada
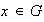 .
.
(b) Para cada
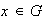 existe
existe
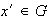 tal que
tal que
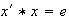 .
.
Demostración.
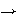 )
Siendo
)
Siendo
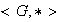 un grupo, existe un
un grupo, existe un
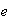 con la condición (a) y cada elemento
con la condición (a) y cada elemento
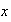 de
de
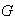 es invertible, es decir, la condición (b) también se da.
es invertible, es decir, la condición (b) también se da.
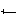 )
Sea
)
Sea
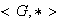 un semigrupo donde se cumplen las condiciones (a) y (b). Demostremos que el
inverso
un semigrupo donde se cumplen las condiciones (a) y (b). Demostremos que el
inverso
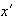 de
de
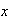 a la izquierda es también a la derecha, es decir, demostremos que
a la izquierda es también a la derecha, es decir, demostremos que
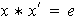 .
.
Sea
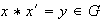 ,
entonces
,
entonces
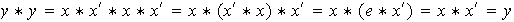 .
.
Ahora, por (b) existe
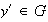 tal que
tal que
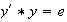 .
Así pues, de
.
Así pues, de
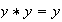 se deduce que
se deduce que
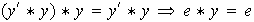
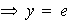 ,
es decir,
,
es decir,
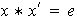 .
.
Ahora probemos que
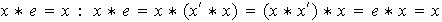 .\
.\
Nota 1. (a) Según
la proposición anterior, si se da un conjunto
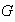 con una operación binaria asociativa es suficiente encontrar en
con una operación binaria asociativa es suficiente encontrar en
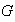 un elemento identidad a la izquierda
un elemento identidad a la izquierda
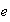 y encontrar para cada
y encontrar para cada
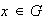 un inverso a la izquierda
un inverso a la izquierda
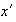 para concluir que
para concluir que
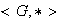 es un grupo cuyo elemento identidad es
es un grupo cuyo elemento identidad es
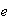 .
.
(b) Es válida la proposición análoga a la anterior para el caso derecho.
(c) No es siempre cierto que si en un semigrupo
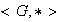 tiene lugar la propiedad (a) a la derecha y la propiedad (b) a la izquierda el
sistema sea un grupo. Por ejemplo, sea
tiene lugar la propiedad (a) a la derecha y la propiedad (b) a la izquierda el
sistema sea un grupo. Por ejemplo, sea
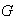 un conjunto no vacío cualquiera y sea
un conjunto no vacío cualquiera y sea
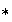 definida por
definida por
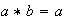 .
.
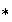 es claramente asociativa. Además cualquier elemento
es claramente asociativa. Además cualquier elemento
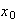 de
de
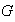 es identidad a la derecha:
es identidad a la derecha:
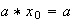 .
Además, dado
.
Además, dado
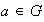 ,
,
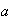 tiene inverso a la izquierda respecto del elemento
tiene inverso a la izquierda respecto del elemento
 .
Sin embargo
.
Sin embargo
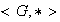 no es un grupo en el caso que
no es un grupo en el caso que
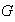 tenga al menos tres elementos distintos
tenga al menos tres elementos distintos
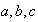 .
.
En efecto, si
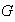 fuera un grupo se tendría la ley cancelativa:
fuera un grupo se tendría la ley cancelativa:
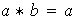
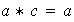
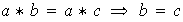
Analogamente, si tiene lugar la propiedad (a) a la izquierda y la propiedad
(b) a la derecha, el sistema
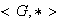 no
es necesariamente un grupo.
no
es necesariamente un grupo.