| Lección 6. |
Grupos - Más Ejemplos sobre Grupos
|
Ejemplo 12. El grupo de
elementos invertibles del semigrupo
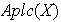 , denotado por
, denotado por
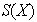 ,
está constituido por las funciones
,
está constituido por las funciones
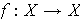 tales que existe
tales que existe
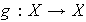 para la cual
para la cual
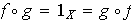 .
En otras palabras,
.
En otras palabras,
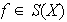 si y sólo si
si y sólo si
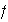 es una función biyectiva.
es una función biyectiva.
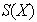 es pues el grupo de todas las funciones biyectivas definidas de
es pues el grupo de todas las funciones biyectivas definidas de
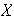 en
en
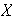 .
En el caso en que
.
En el caso en que
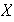 sea un conjunto finito de
sea un conjunto finito de
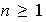 elementos,
elementos,
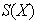 se denota por
se denota por
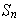 . Este grupo será estudiado en detalle en el Capítulo VI. Para el
caso
. Este grupo será estudiado en detalle en el Capítulo VI. Para el
caso
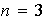 vamos a ilustrar todos los elementos de
vamos a ilustrar todos los elementos de
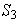 :
:
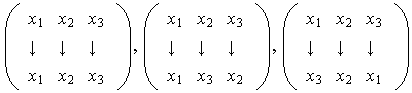

Observe que este grupo no es conmutativo.
Ejemplo 13. Sea
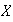 un conjunto no vacío y sea
un conjunto no vacío y sea
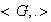 un grupo con elemento identidad
un grupo con elemento identidad
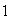 .
Sea
.
Sea
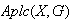 el conjunto de funciones de
el conjunto de funciones de
 en
en
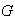 .
Se define en este conjunto la siguiente operación:
.
Se define en este conjunto la siguiente operación:
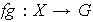
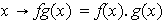
donde
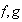 son elementos de
son elementos de
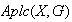 y
y
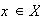 .
Esta operación convierte a
.
Esta operación convierte a
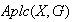 en un grupo. Nótese que el elemento identidad
es la función
en un grupo. Nótese que el elemento identidad
es la función
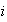 que asigna a cada elemento
que asigna a cada elemento
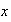 de
de
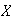 el elemento identidad
el elemento identidad
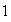 de
de
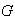 .
El inverso de la función
.
El inverso de la función
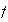 es una función
es una función
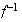 tal que
tal que
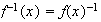 ,
para cada
,
para cada
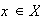 .
.
Ejemplo 14. Del
álgebra lineal
podemos tomar el siguiente ejemplo: Sea
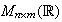 el conjunto de matrices rectangulares de
el conjunto de matrices rectangulares de
 filas y
filas y
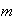 columnas con la \textoperación habitual de
suma definida sobre las entradas de las matrices. Esta operación
convierte a
columnas con la \textoperación habitual de
suma definida sobre las entradas de las matrices. Esta operación
convierte a
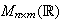 en un grupo conmutativo, en el cual el elemento identidad es la matriz nula y
el inverso aditivo de una matriz
en un grupo conmutativo, en el cual el elemento identidad es la matriz nula y
el inverso aditivo de una matriz
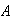 es la matriz con entradas de signo contrario a las entradas de la matriz
es la matriz con entradas de signo contrario a las entradas de la matriz
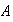 .
.
Ejemplo 15. En álgebra elemental se
consideran los polinomios
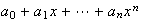 con coeficientes reales, la colección de todos estos polinomios
(
con coeficientes reales, la colección de todos estos polinomios
(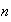 no es fijo !) se denota por
no es fijo !) se denota por
![$\QTR{Bbb}{R}[x]$](graphics/cap1s2c__48.png) y constituye un grupo respecto a la adición de polinomios mediante
reducción de términos semejantes. El polinomio nulo es el elemento
identidad y el inverso aditivo de un polinomio se obtiene cambiandole el signo
a cada uno de sus coeficientes.
y constituye un grupo respecto a la adición de polinomios mediante
reducción de términos semejantes. El polinomio nulo es el elemento
identidad y el inverso aditivo de un polinomio se obtiene cambiandole el signo
a cada uno de sus coeficientes.