| Ejercicios |
Ejercicio 19. Cada una de las siguientes tablas definen operaciones binarias internas de las cuales se saben que son asociativas. Comprobar que ellas definen grupos:
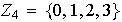
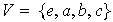
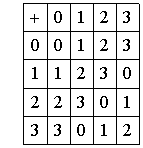

Es
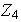 un grupo conmutativo? Es
un grupo conmutativo? Es
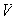 un grupo conmutativo?
un grupo conmutativo?
Es
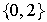 un subgrupo de
un subgrupo de
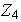 ?
Es
?
Es
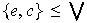 ?
?
Es
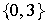 un subgrupo de
un subgrupo de
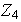 ?
Es
?
Es
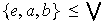 ?
?
Ejercicio 20. Sea
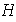 un subconjunto finito no vacío de un grupo
un subconjunto finito no vacío de un grupo
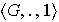 y sea
y sea
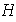 cerrado respecto a la operación; es decir,
cerrado respecto a la operación; es decir,
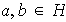 implica
implica
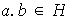 . Entonces demostrar que
. Entonces demostrar que
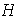 es un subgrupo de
es un subgrupo de
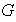 .
.
Ejercicio 21. Sean
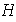 y
y
 subgrupos del grupo
subgrupos del grupo
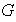 . Probar que
. Probar que
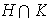 es un subgrupo de
es un subgrupo de
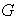 .
.
Ejercicio 22. Sea
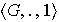 un grupo. Se llama orden del grupo y se denota por
un grupo. Se llama orden del grupo y se denota por
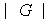 o por
o por
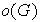 al cardinal del conjunto
al cardinal del conjunto
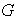 . Si
. Si
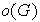 es finito, se dice que el grupo es finito. En caso contrario, se dice que
es finito, se dice que el grupo es finito. En caso contrario, se dice que
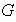 es infinito. Probar que si
es infinito. Probar que si
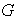 no es conmutativo, entonces
no es conmutativo, entonces
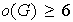 .
.
Ejercicio 23. Sea
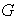 un grupo y
un grupo y
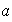 un elemento de
un elemento de
 .
Definamos
.
Definamos
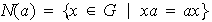 .
.
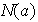 se llama el normalizador de
se llama el normalizador de
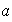 en
en
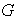 . Demostrar que
. Demostrar que
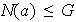 .
.
Ejercicio 24. Sea
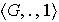 un grupo abeliano. Probar que el conjunto
un grupo abeliano. Probar que el conjunto
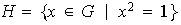 es un subgrupo de
es un subgrupo de
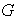 .
.
Ejercicio 25. Sea
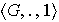 un grupo y
un grupo y
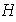 un subgrupo no vacío de
un subgrupo no vacío de
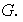 Probar que
Probar que
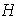 es un subgrupo de
es un subgrupo de
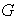 si y sólo si se cumple la condición
si y sólo si se cumple la condición
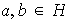 implica
implica
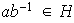
Ejercicio 26. Sea
 el grupo de matrices de orden 2 con entradas reales con respecto a la
adición, y sea
el grupo de matrices de orden 2 con entradas reales con respecto a la
adición, y sea
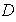 el conjunto de matrices de
el conjunto de matrices de
 que son diagonales, es decir
que son diagonales, es decir
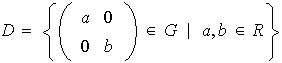 .
Demostrar que
.
Demostrar que
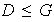 .
.
Ejercicio 27. Sea
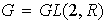 el grupo lineal general de orden 2 sobre los números reales, es decir,
el grupo lineal general de orden 2 sobre los números reales, es decir,
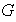 es el grupo de elementos invertibles del semigrupo multiplicativo
es el grupo de elementos invertibles del semigrupo multiplicativo
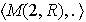 .
Sea
.
Sea
 el
subconjunto de
el
subconjunto de
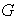 constituido por las matrices de determinante
constituido por las matrices de determinante
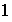 :
:
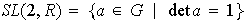 .
Demostrar que
.
Demostrar que
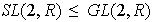 .
.