| Lección 14. |
Clases Laterales. Teorema de Lagrange
|
Sea
 un grupo con un número finito de elementos y sea
un grupo con un número finito de elementos y sea
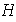 un subgrupo de
un subgrupo de
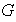 .
Desde luego
.
Desde luego
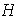 también es un grupo con un número finito de elementos. Resulta
interesante preguntarnos que relación guardan la cantidad de elementos
del subgrupo
también es un grupo con un número finito de elementos. Resulta
interesante preguntarnos que relación guardan la cantidad de elementos
del subgrupo
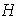 y la cantidad de elementos del grupo
y la cantidad de elementos del grupo
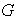 .
En esta lección mostraremos que el número de elementos de
.
En esta lección mostraremos que el número de elementos de
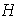 divide al número de elementos del grupo dado
divide al número de elementos del grupo dado
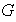 .
.

Proposición 16. Sea
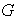 un grupo cualquiera y sea
un grupo cualquiera y sea
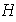 un subgrupo de
un subgrupo de
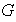 .
La relacion entre los elementos de
.
La relacion entre los elementos de
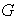 definida por
definida por
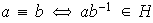 ,
,
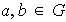 (1)
(1)
es una relación de equivalencia en
 .
Cuando dos elementos
.
Cuando dos elementos
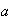 y
y
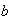 de
de
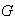 están relacionados mediante esta relación
están relacionados mediante esta relación
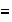 diremos que
diremos que
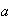 es congruente con
es congruente con
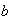 módulo
módulo
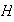 .
.
Demostración:
Reflexiva: sea
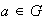 entonces
entonces
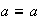 ya que
ya que
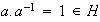 por ser
por ser
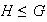 .
.
Simétrica: Sean
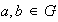 tales que
tales que
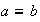 . Entonces
. Entonces
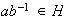 ;
, por ser
;
, por ser
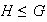 tenemos que
tenemos que
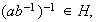 pero
pero
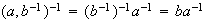 , o sea que
, o sea que
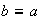 .
.
Transitiva: Sean
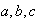 elementos de
elementos de
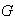 tales que
tales que
 y
y
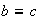 .
Entonces
.
Entonces
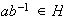 y
y
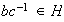 . De ahí que resulta que
. De ahí que resulta que
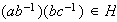 , es decir
, es decir
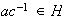 y por lo tanto
y por lo tanto
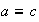 . Esto completa la demostración de la proposición.
. Esto completa la demostración de la proposición.
Nota 2. Si para el
grupo G estamos usando la notación aditiva entonces la relacion
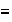 se define como
se define como
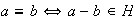 .
.
Es conocido que cualquier relación de equivalencia
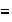 definida sobre un conjunto
definida sobre un conjunto
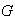 determina una partición de dicho conjunto en clases de equivalencia
disyuntas entre si y la reunión de las cuales da el conjunto
determina una partición de dicho conjunto en clases de equivalencia
disyuntas entre si y la reunión de las cuales da el conjunto
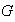 .
Así pues, para el caso que estamos tratando, sea
.
Así pues, para el caso que estamos tratando, sea
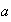 un elemento cualquiera del grupo
un elemento cualquiera del grupo
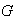 .
La clase de eqivalencia a la cual pertenece el elemento
.
La clase de eqivalencia a la cual pertenece el elemento
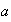 será denotada por
será denotada por
![$[a]$](graphics/cap1s4__52.png) y esta constituída por todos los elementos
y esta constituída por todos los elementos
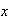 de
de
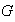 con los cuales
con los cuales
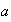 está relacionado mediante la relación
está relacionado mediante la relación
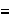 ; es decir:
; es decir:
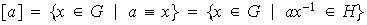
Finalmente y como lo dijimos arriba, la reunión de las clases
determinadas por la relación
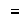 es todo el conjunto (grupo)
es todo el conjunto (grupo)
 :
:
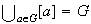
Lógicamente la cantidad de clases puede ser muy grande. Puesto que la
relación
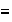 definida en
definida en
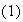 fue dada por medio del subgrupo
fue dada por medio del subgrupo
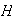 ,
cabe preguntarnos si entre cada clase
,
cabe preguntarnos si entre cada clase
![$[a]$](graphics/cap1s4__64.png) y el subgrupo
y el subgrupo
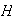 hay alguna relación.
hay alguna relación.
Proposición 17. Sea G un grupo,
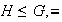 la relación de equivalencia definida en
la relación de equivalencia definida en
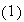 y sea
y sea
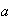 un elemento cualquiera de
un elemento cualquiera de
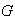 . Entonces:
. Entonces:
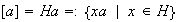 .
En particular,
.
En particular,
![$[1]=H.1=H$](graphics/cap1s4__71.png)
Demostración: Sea
 ,
entonces
,
entonces
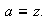 Por ser
Por ser
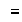 una relacion simétrica tenemos que
una relacion simétrica tenemos que
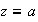 y por eso
y por eso
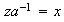 ,
con
,
con
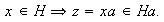 Hemos probado que
Hemos probado que
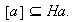 Sea
Sea
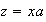 un elemento de
un elemento de
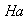
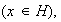 entonces
entonces
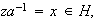 o sea
o sea
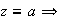
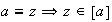 .
Esto completa la prueba de nuestra afirmación.
.
Esto completa la prueba de nuestra afirmación.
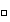
Definición 14. Sea
 un grupo,
un grupo,
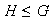 y
y
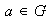 . El conjunto
. El conjunto
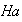 se llama la clase lateral derecha del elemento
se llama la clase lateral derecha del elemento
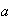 módulo
módulo
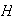 .
.
La afirmación anterior muestra en particular que la clase del elemento
identidad 1 del grupo G coincide con el subgrupo H. Es decir [1] y H tienen la
misma "cantidad" de elementos. A continuación probaremos que todas las
clases tienen la misma cantidad de elementos que
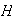 y por ende todas las clases de equivalencia tienen la misma cantidad de
elementos.
y por ende todas las clases de equivalencia tienen la misma cantidad de
elementos.
Proposición 18. Sea
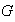 un grupo,
un grupo,
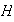 un subgrupo de
un subgrupo de
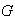 y
y
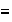 la relación de equivalencia definida (1) por medio del subgrupo
la relación de equivalencia definida (1) por medio del subgrupo
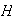 .
Entonces todas las clases de equivalencia determinadas por
.
Entonces todas las clases de equivalencia determinadas por
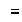 tienen el mismo cardinal que el subgrupo
tienen el mismo cardinal que el subgrupo
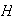 .
En consecuencia, todas las clases de equivalencia determinadas por
.
En consecuencia, todas las clases de equivalencia determinadas por
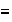 tienen el mismo cardinal.
tienen el mismo cardinal.
Demostración: Sea
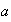 un elemento cualquiera de
un elemento cualquiera de
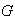 . Entonces
. Entonces
![$[a]=Ha.$](graphics/cap1s4__103.png) La función
La función
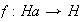 ,
,
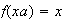 ,
,
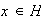 ,
es biyectiva. En efecto, claramente
,
es biyectiva. En efecto, claramente
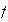 es sobreyectiva. Supóngase que
es sobreyectiva. Supóngase que
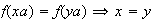 y así
y así
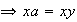 , con lo cual
, con lo cual
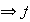 es
inyectiva.
es
inyectiva.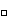
Estamos ya en condiciones de demostrar el Teorema de Lagrange para grupos finitos.
Teorema de Lagrange.
Sea
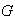 un grupo finito y sea
un grupo finito y sea
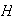 un subgrupo cualquiera de
un subgrupo cualquiera de
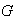 .
Denotemos por
.
Denotemos por
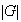 el número de elementos del grupo
el número de elementos del grupo
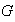 y por
y por
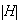 el número de elementos del subgrupo
el número de elementos del subgrupo
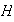 . Entonces,
. Entonces,
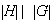 .
.
Demostración: Puesto que
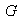 es finito entonces
es finito entonces
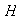 determina un número finito de clases de equivalencia en
determina un número finito de clases de equivalencia en
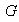 . Sea
. Sea
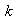 el número de clases de equivalencia definidas en el grupo
el número de clases de equivalencia definidas en el grupo
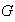 ;
como estas clases son disyuntas, y además todas tienen
;
como estas clases son disyuntas, y además todas tienen
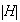 elementos, entonces
elementos, entonces
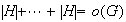 , es decir,
, es decir,
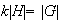 ,
así
,
así
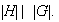 ▫
▫
Definición 15. Sea
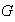 un grupo cualquiera y sea
un grupo cualquiera y sea
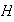 un subgrupo de
un subgrupo de
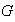 .
El cardinal del conjunto de clases de equivalencia determinado por el subgrupo
H mediante la relación definida en
.
El cardinal del conjunto de clases de equivalencia determinado por el subgrupo
H mediante la relación definida en
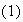 se llama el índice del subgrupo
se llama el índice del subgrupo
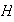 en el grupo
en el grupo
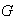 y se simboliza por
y se simboliza por
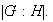 Cuando
Cuando
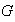 es finito se tiene que
es finito se tiene que
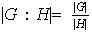
Ejemplo 26. 1) Sea
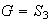 y sea
y sea
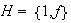 ,
donde
,
donde
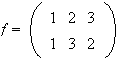 .
Calculemos
.
Calculemos
 y además determinemos el conjunto de clases laterales de
y además determinemos el conjunto de clases laterales de
 .
.
Por el Teorema de Lagrange
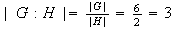
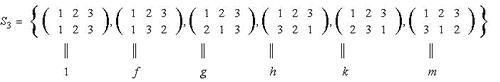
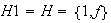 ;
;
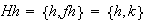
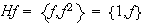
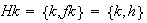
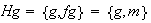
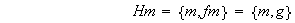
Nótese que
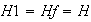 ;
;
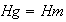 ;
;
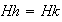 ,
es decir se tienen 3 clases de equivalencia tal como lo había
pronosticado el Teorema de Lagrange. Obsérvese que una clase de
equivalencia, o en otras palabras, una clase lateral derecha no es general un
subgrupo del grupo dado.
,
es decir se tienen 3 clases de equivalencia tal como lo había
pronosticado el Teorema de Lagrange. Obsérvese que una clase de
equivalencia, o en otras palabras, una clase lateral derecha no es general un
subgrupo del grupo dado.
2)
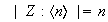 ,
para
,
para
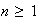 ;
;
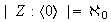 .
.