| Lección 13. |
Subgrupos - Mas Sobre Generación de Subgrupos
|
Proposición 14. Sea G un grupo cualquiera. Entonces
1)
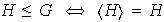
2)
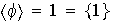
3)
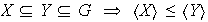
4)
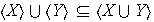. En general la union de subgrupos no es un subgrupo.
Demostración.
1) y 2) son evidentes.
3)
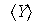es un subgrupo de G que contiene a
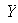
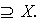Por
lo tanto
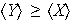
4)
;
.
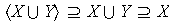Análogamente
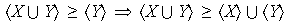. Esto concluye la prueba de la proposición
Proposición 15. Sea
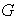un grupo finitamente generado y sea H un subgrupo propio de
.
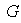Entonces existe un subgrupo maximal de
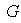que contiene a
.
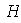Demostración. Sea
un sistema finito de generadores de
.
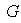Sea
=
.
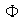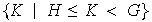Lógicamente
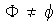ya que
.
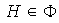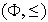es un conjunto parcialmente ordenado. Sea
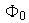una cadena de
.
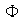Sea
,
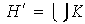la unión de los subgrupos
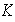de esta cadena. Nótese que
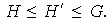En efecto, Sean
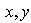
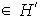; entonces existen
,
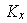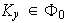tales que
,
.
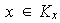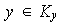Como
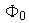es totalmente ordenado, entonces podemos suponer que
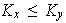y entonces
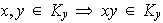con lo cual
.
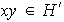Además,
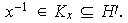
Ahora, como
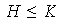para cada
,
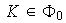entonces
.
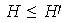Se debe observar que
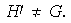En efecto, si
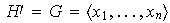Entonces
con
.
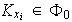Existe entonces
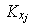tal que
;
,
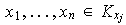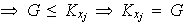lo cual es contradictorio. Así pues,
.
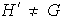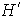es cota superior para
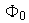en
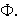De acuerdo al Lema de Zorn,
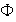tiene elemento maximal
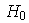el cual es obviamente subgrupo maximal de
