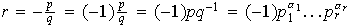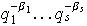| Lección 12. |
Subgrupos - Ejemplos
|
Ejemplo 23. Todo grupo cíclico G con
generador a es un grupo finitamente generado con conjunto generador
:
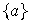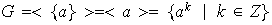
Nótese por ejemplo que
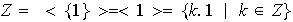
Ejemplo 24. Sea
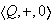el grupo aditivo de los números racionales entonces:
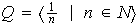
En efecto sea
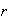un racional. Si
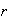es positivo entonces podemos considerar que
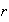es de la forma
,
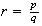donde
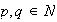
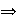
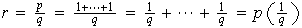
Si
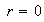entonces
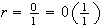Si
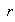es negativo entonces podemos suponer que
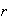es de la forma
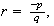con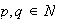 
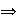
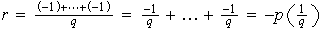
Ejemplo 25. Sea
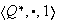el grupo multiplicativo de los números racionales no nulos, entonces:
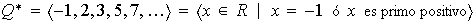
Sea
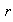racional no nulo. Si
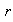es positivo entonces
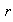es de la forma
con 
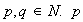y
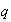se pueden descompooner en factores primos:
,
,
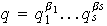donde
,
(Es posible que
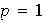o
)
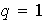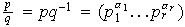
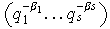
Si
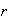es negativo podemos suponer que
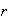es de la forma
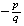con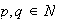 
entonces:
