| Lección 11. |
Subgrupos - Generación de Subgrupos
|
Dado un subconjunto
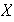de un grupo
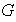se desea establecer si existe un subgrupo
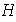en
,
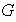distinto de
,
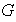que contenga a
.
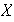En caso de que podamos determinar una colección de tales subgrupos
,
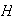conviene preguntar cuál es el grupo más pequeño de
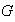que contiene
.
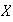Antes de responder a estas preguntas aclaremos primero el término
"subgrupo más pequeño".
Proposición 10. Sea
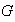un grupo. En el conjunto de todos los subgrupos de
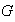la relación "ser grupo de" determina un orden parcial.
Como en cualquier conjunto parcialmente ordenado, podemos hablar de subgrupo maximal y subgrupo minimal de un grupo dado.
Definición 12. Sea
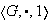un grupo y sea
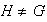un subgrupo de
.
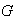(1) Se dice que que
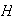es un subgrupo maximal de
,
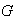si para cada subgrupo
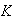de
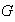se tiene la implicación
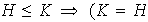ó
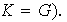
(2) Se dice que
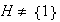es un subgrupo minimal de
,
si por cada subgrupo
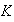de
se tiene la implicación
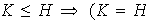ó
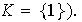
Ejemplo 22. Los subgrupos maximales del grupo
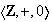son de la forma
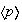donde
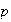es primo. Además,
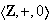no posee subgrupos minimales.
Queremos responder ahora las preguntas planteadas al principio de la lección:
Proposición 11. Sea
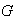un grupo y
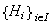una familia de subgrupos de
.
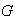Entonces la intersección de dicha familia
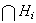es un subgrupo de
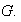
Proposición 12. Sea
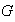un grupo y sea
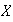un subconjunto cualquiera de
.
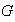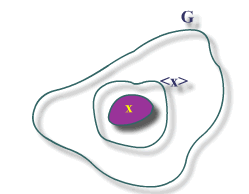
Existe en
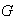un subgrupo, denotado por
,
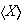que contiene a
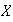y que es el más \textpequeño subgrupo de
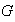con dicha propiedad.
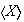coincide con la intersección de la familia de todos los subgrupos de
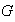que contienen a
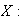
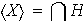
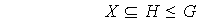
Demostración. Evidente.
Corolario 1.
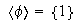
Demostración.
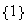es el subgrupo más pequeño de
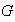que contiene a
.
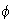La afirmación anterior no permite de una manera concreta determinar los
elementos del grupo
,
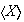ya que sería necesario determinar todos los subgrupos de
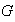que contienen
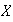y luego efectuar la intersección.
Se tiene en cambio el siguiente resultado:
Proposición 13. Sea
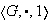un grupo, y sea
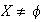un subconjunto de
.
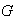Entonces:
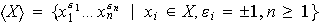
Demostracion. Sea
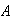el conjunto de la derecha de la igualdad anterior. Entonces:
(a)
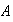es un subgrupo de
:
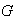sean
,
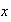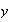dos elementos de A. Entonces
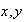son de la forma:
...
...
...,
...,
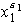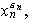
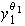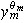
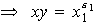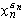
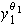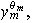
y por tanto el producto
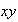tiene la forma de los elementos del conjunto
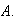Es claro que el inverso de un elemento de
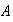tiene la forma de los elementosde
.
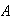(b)
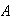contiene al conjunto
:
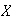en efecto cada elemento
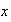de
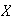tiene la forma de los elementos de
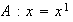
(c) De las dos últimas afirmaciones se obtiene que
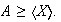
(d) De otra parte,
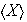
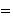
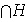
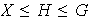
entonces, cada
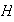que contiene a
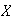contiene a todos los productos de elementos de
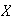o inversos de elementos de
,
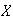así pues, cada
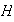que contiene a
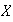contiene también a
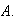
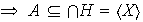
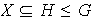
Corolario 2.
Sea
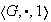un grupo abeliano, y
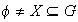Entonces:
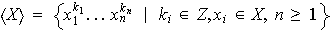
En notación aditiva tenemos
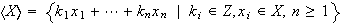
Demostración. Siendo
abeliano para cada elemnto
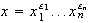de
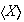podemos agrupar las potencias de elementos iguales.
Definición 13. Sea
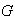un grupo y sea
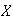un suconjunto de
.
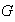El subgrupo más pequeño de
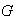que contiene
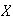se denomina también subgrupo generado por el subconjunto
;
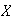a
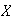se le demnomina conjunto de generadores de
.
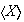Es posible que para cierto subconjunto X,
.
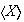
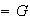En ese caso se dice que
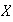genera al grupo
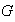o también que
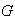es generado por el subconjunto
.
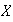Si
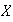es finito y
se dice que
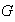es un grupo finitamente generado