| Lección 10. |
Subgrupos - El Grupo Z
|
Ejemplo 21.
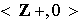es un grupo cíclico y todos sus subgrupos son cíclicos:
Sea
.
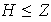Si
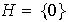es el subgrupo trivial nulo, entonces claramente
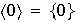y
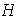es cíclico. Supóngase que
.
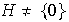Entonces existe
,
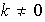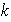
entero,
.
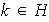Si
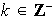entonces
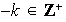y
.
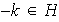Así pues, el conjunto
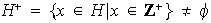
Por ser el conjunto
(
)
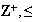bien ordenado, existe un mínimo entero positivo
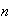en
.
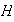Queremos probar que
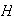coincide con el subgrupo ciclico generado por
,
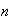es decir,
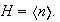
En efecto, sea
.
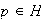Existen enteros
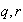tales que
De aquí resulta
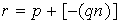
Si
,
entonces
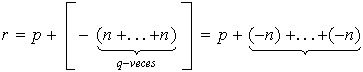
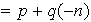
Como
y
,
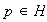entonces
.
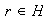Por la escogencia de
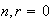y así
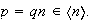
Si
,
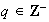entonces
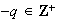y en total
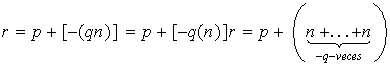
Como
,
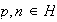entonces
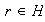y nuevamente
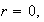con lo cual
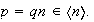
Si
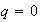entonces
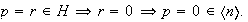
En los tres casos hemos probado que
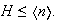Puesto que
,
la otra inclusión es obvia.
Se ha demostrado que cada subgrupo
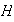de
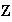es cíclico y generado por el menor entero positivo
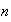contenido en
.
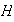Además,
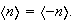Así pues, los subgrupos de
son:
