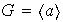| Lección 9. |
Subgrupos\Cíclicos
|
Ejemplo 20. Para un semigrupo multiplicativo
fueron definidas las potencias enteras positivas (ver la
Proposición 1). Pretendemos ahora extender estas
potencias a todos los enteros y presentar la correspondiente notación
para el caso de los grupos aditivos.
Teniendo en cuenta esta definición, es posible demostrar por inducción matemática las siguientes relaciones en cualquier grupo:
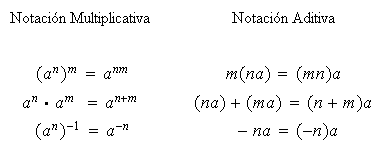
para cualesquiera
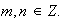
Sea
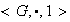un grupo y sea
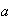un elemento cualquiera de
.
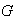Simbolizamos por
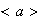el conjunto de todos los elementos de
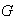que son potencias enteras de
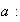
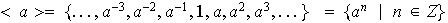
Nótese que
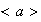es un subgrupo de
:
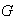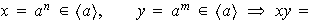
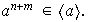
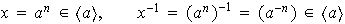
Claramente:
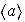es no vacío ya que
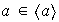
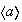se denomina el subgrupo cíclico de
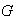generado por el elemento
.
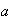En notación aditiva tenemos que el subgrupo cíclico generado por
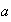es :
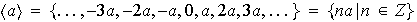
Definición 11. Sea
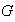un grupo, se dice que
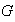es cíclico si existe un elemento
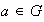tal que el subgrupo cíclico generado por
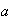coincide con todo el grupo
.
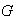