| Lección 8. |
Subgrupos - Teoría
|
Dado un grupo
y un subconjunto no vacío
de
,
,
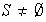es intresante conocer si bajo la misma operación binaria de
,
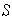tiene
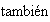estructura de grupo. Lo primero que deberá cumplirse es que el producto
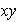de dos elementos del conjunto
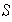debe permanecer también en
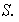
Gráfica 1
Definición 10. Sea
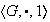un grupo y
,
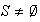un subconjunto no vacío de
.
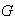Se dice que
es un subgrupo de
si
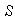bajo la operación
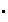de
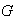tiene estructura de grupo y escribimos en este caso
.
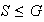De acuerdo a esta definición y a la definición de grupo
tendríamos que verificar cuatro condiciones para garantizar que un
subconjunto
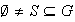constituye un subgrupo:
(1) El producto de dos elementos
de
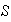está también en
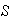
(2) La operación
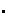es asociativa en
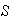
(3) En
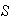hay elemento identidad con respecto a la operación
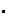
(4) Cada elemento
de
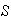tiene un inverso
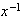en
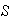respecto a la operación
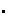y al elemento identidad encontrado en (3)
Sin embargo como lo muestra la siguiente proposición sólo hay que comprobar el cumplimiento de dos condiciones.
Proposición 8. Sea
un grupo y
,
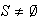un subconjunto no vacío de
,
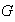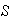bajo la operación
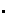es un subgrupo de
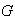si y sólo si se cumplen las siguientes condiciones
(a)
,
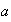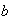
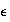
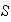implica
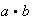
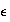
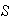
(b)
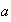
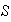implica
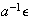
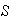
Demostración
)
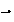Si
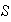es un subgrupo de
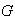entonces según la definición,
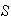bajo la operación
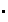de
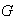es un grupo. Por lo tanto
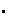es una operación binaria en
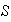con lo cual se garantiza la condición (a) Puesto que
,
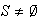sea entonces
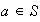. Sabemos entonces que las ecuaciones
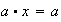y
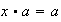tienen soluciones \textúnicas en el grupo
.
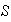Pero estas condiciones pueden ser consideradas en el grupo
.
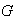Por lo tanto,
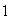que es la solución de ellas en
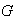debe ser tambien la solución en
,
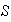es decir,
.
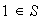Ahora las ecuaciones
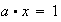y
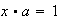también tienen soluciones únicas tanto en
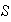como en
.
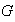Esto indica que
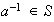y la condición (b) está demostrada.
)
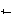La condición (a) indica que
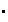define en
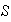una operación binaria interna. La asociatividad de
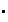en
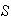es evidente ya que ello se cumple para todos los elementos de
,
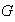en particular, para los elementos de
.
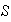Sea
(
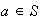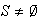). Entonces, según (b)
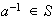y según (a)
,
\
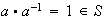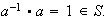Ejemplo 16. Subgrupos triviales: Sea
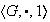un grupo. Entonces,
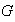tiene al menos dos subgrupos llamados sus subgrupos triviales
,
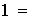
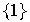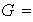
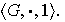
Ejemplo 17..
.
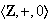
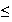
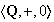
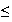
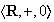
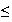
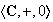Esta cadena de subgrupos induce la siguiente afirmación:
Proposición 9. Sea
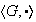un grupo,
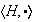un subgrupo de
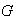y
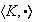un subgrupo de
,
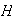entonces
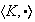es un subgrupo de
.
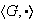Ejemplo 18.
.
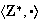
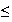
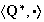
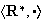
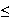
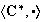Ejemplo 19. Sea
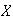un conjunto no vacío y sea
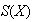el grupo de permutaciones del conjunto
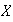bajo la operación de composición de funciones. Sea
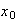un elemento fijo del conjunto
.
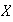Sea
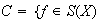
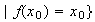el conjunto de funciones que dejan fijo el punto
.
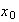Entonces
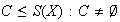ya que
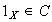
Sean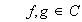
entonces
,
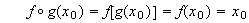así
pues
.
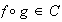Sea
,
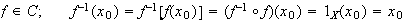por tanto
.
Como caso particular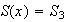, sea
y sea
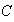el conjunto de permutaciones que dejan fijo el punto 3 :
