| Lección 1. |
p-Grupos Abelianos Finitos
|
Comenzamos probando que todo grupo finito
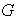 de orden
de orden
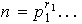
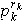 , es suma directa de sus subgrupos de Sylow si y sólo si estos son
normales. En el caso de ser
, es suma directa de sus subgrupos de Sylow si y sólo si estos son
normales. En el caso de ser
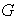 abeliano esta condición se da automáticamente y podemos enunciar el
siguiente teorema.
abeliano esta condición se da automáticamente y podemos enunciar el
siguiente teorema.
Teorema 1. Sea
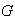 un grupo finito de orden
un grupo finito de orden
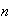 ,
,
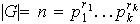 ;
;
 primos diferentes y
primos diferentes y
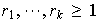
Entonces,
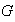 es suma directa de sus subgrupos de Sylow si y sólo si estos son normales
en
es suma directa de sus subgrupos de Sylow si y sólo si estos son normales
en
 :
:
 ,,,,,(1)
,,,,,(1)
donde
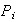 es el
es el
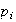 -subgrupo
de Sylow de
-subgrupo
de Sylow de
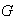 ,
,
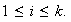 En particular, si
En particular, si
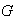 es abeliano, entonces
es abeliano, entonces
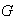 es suma directa interna de sus subgrupos de Sylow.
es suma directa interna de sus subgrupos de Sylow.
Demostración.
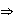 )
Si
)
Si
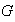 es suma directa de sus subgrupos de Sylow, entonces por la definición de
suma directa, cada sumando es necesariamente subgrupo normal de
es suma directa de sus subgrupos de Sylow, entonces por la definición de
suma directa, cada sumando es necesariamente subgrupo normal de
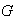 .
.
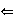 )
Para
)
Para
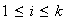 ,
sea
,
sea
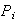 un
un
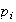 -subgrupo
de Sylow de
-subgrupo
de Sylow de
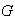 tal que
tal que
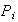 es un subgrupo normal de
es un subgrupo normal de
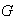 .
Entonces
.
Entonces
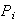 es único. Probaremos entonces que (1) se cumple. Veremos que cada
elemento
es único. Probaremos entonces que (1) se cumple. Veremos que cada
elemento
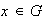 tiene una representación única en la forma
tiene una representación única en la forma
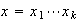 ,
donde
,
donde
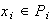 ,
,
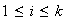 .
.
a) Por razones de orden de sus elementos, para
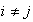 se tiene que
se tiene que
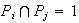 .
.
b) A partir de a) se obtiene que para
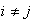 los elementos de
los elementos de
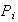 conmutan con los de
conmutan con los de
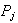 .
.
c) El neutro
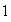 de
de
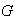 tiene representación única: sean
tiene representación única: sean
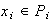 ,
,
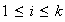 tales que
tales que
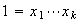 .
Sea
.
Sea
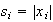 ,
entonces
,
entonces
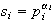 ,
,
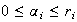 .
Sea
.
Sea
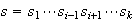 ,
entonces
,
entonces
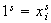 ,
luego
,
luego
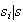 y por lo tanto
y por lo tanto
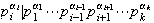 .
Esto implica que
.
Esto implica que
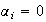 ,
luego
,
luego
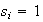 ,
es decir,
,
es decir,
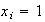 ,
para cada
,
para cada
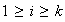 .
.
d) Cada elemento
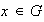 se puede representar en la forma única anunciada: sea
se puede representar en la forma única anunciada: sea
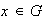 de orden
de orden
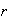 de tal forma que
de tal forma que
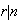 y
y
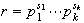 ,
donde
,
donde
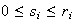 con
con
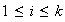 .
Sea
.
Sea
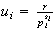 ,
entonces
,
entonces
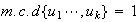 .
Existen entonces enteros
.
Existen entonces enteros
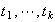 tales que
tales que
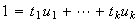 ,
sea
,
sea
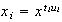 ,
,
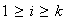 .
Nótese que
.
Nótese que
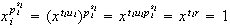 ;
luego
;
luego
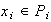 .
Nótese ahora que
.
Nótese ahora que
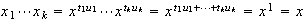 .
A partir de b) y c) se obtiene que esta representación es única.\
.
A partir de b) y c) se obtiene que esta representación es única.\
Corolario 1. Sea
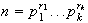 .
Entonces,
.
Entonces,
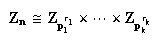
El objetivo central en la descripción de los grupos abelianos finitos
consiste en expresar
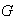 como suma directa de subgrupos de estructura simple y conocida, como por
ejemplo a tráves de subgrupos cíclicos. Desde luego que sobre estos
subgrupos habrá que colocar alguna
como suma directa de subgrupos de estructura simple y conocida, como por
ejemplo a tráves de subgrupos cíclicos. Desde luego que sobre estos
subgrupos habrá que colocar alguna
 ya que de lo contrario la descomposición no sería única.
Nótese por ejemplo que
ya que de lo contrario la descomposición no sería única.
Nótese por ejemplo que
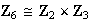 .
.
Nuestro objetivo inmediato es estudiar los
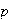 -grupos
abelianos finitos, es decir, los grupos abelianos cuyo orden es de la forma
-grupos
abelianos finitos, es decir, los grupos abelianos cuyo orden es de la forma
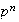 ,
,
Proposición 1. Si
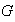 es un grupo cíclico de orden
es un grupo cíclico de orden
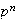 ,
entonces
,
entonces
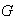 no se puede descomponer en suma directa de subgrupos cíclicos de orden
menor, es decir,
no se puede descomponer en suma directa de subgrupos cíclicos de orden
menor, es decir,
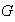 es irreducible.
es irreducible.
Demostración. Sabemos que
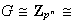
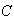
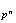 .
Probemos inicialmente que los únicos subgrupos de
.
Probemos inicialmente que los únicos subgrupos de
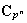 son los subgrupos de la cadena
son los subgrupos de la cadena
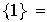
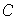
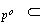
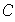
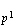
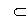
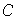
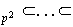
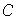
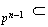
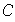
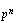
Sea
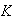
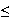
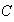
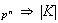
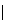
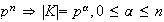 ;
sea
;
sea
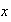
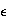
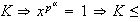
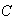
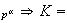
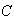
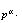
Ahora si existiera
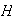 ,
,
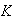 en
en
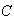
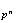 tales que
tales que
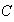
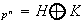 entonces
entonces
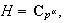
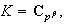
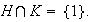 Para
Para
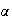 y
y
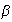 dados se tiene que
dados se tiene que
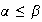 o
o
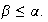 En el primer caso
En el primer caso
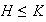 y
y
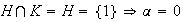 y
y
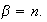 En el segundo caso
En el segundo caso
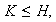
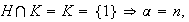
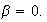 En total la única descomposición de
En total la única descomposición de
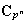 es la trivial:
es la trivial:
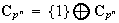 .\
.\
Ejemplo 1.
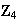 y
y
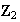

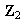 no son isomorfos.
no son isomorfos.
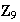 y
y
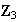

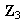 no son isomorfos.
no son isomorfos.
Teorema 2. Cada
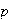 -grupo
abeliano finito
-grupo
abeliano finito
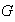 es suma directa de subgrupos cíclicos.
es suma directa de subgrupos cíclicos.
Demostración. Sea
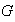 un
un
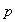 -grupo
abeliano finito.
Entonces
-grupo
abeliano finito.
Entonces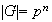 .
Si
.
Si
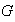 es cíclico entonces según la proposición anterior la única
descomposición de
es cíclico entonces según la proposición anterior la única
descomposición de
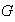 es la trivial:
es la trivial:
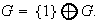
Supóngase que
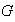 no es cíclico. En este caso la demostración se efectua por
inducción. Supóngase que el teorema ha sido demostrado para los
no es cíclico. En este caso la demostración se efectua por
inducción. Supóngase que el teorema ha sido demostrado para los
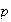 -grupos
abelianos de orden
-grupos
abelianos de orden
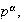
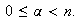
Sea
 un grupo abeliano de orden
un grupo abeliano de orden
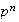 .
Cada elemento
.
Cada elemento
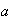 de
de
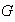 ,
,
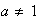 ,
tiene orden de la forma
,
tiene orden de la forma
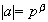 ,
,
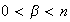 .
Escojamos un
.
Escojamos un
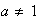 que tenga orden maximal
que tenga orden maximal
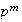 (esto quiere decir que no existe
(esto quiere decir que no existe
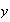 en
en
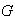 tal que
tal que
 ).
).
Consideremos el grupo cociente
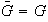
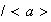 .
Puesto que
.
Puesto que
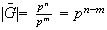 y
y
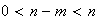 entonces según la hipótesis inductiva
entonces según la hipótesis inductiva
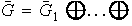
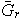
donde cada
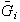 es un subgrupo cíclico de
es un subgrupo cíclico de
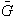 de orden
de orden
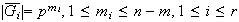 ;
además
;
además

Sea
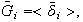
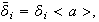
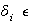
 ,
,
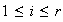 .
Sería lógico pensar que
.
Sería lógico pensar que
 .
Sin embargo no es este el caso, pero con ayuda de los elementos
.
Sin embargo no es este el caso, pero con ayuda de los elementos
 construiremos otros
construiremos otros
 y para ello probaremos que
y para ello probaremos que

Nótese que para cada
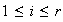 ,
,
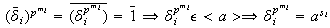 con
con
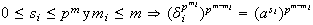
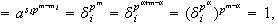 donde
donde
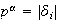 (
(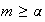 ya que
ya que
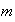 es maximal)
es maximal)
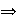
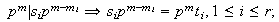
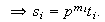
Definimos entonces
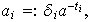
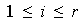
Nótese que para cada
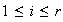
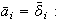 En efecto,
En efecto,
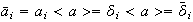 ya que
ya que
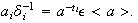 De aquí obtenemos que
De aquí obtenemos que
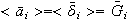 ,
,
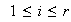 .
Por lo tanto,
.
Por lo tanto,

Sea
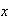 un elemento cualquiera de
un elemento cualquiera de
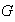 .
Entonces
.
Entonces
 donde
donde
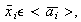
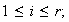
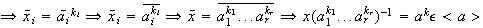
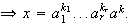
Se ha probado que cada elemento
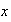 de
de
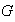 se expresa como producto de elementos de
se expresa como producto de elementos de
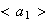 ,...,
,...,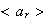 y
y
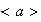 .
.
Queda por demostrar que la representación es única:
Para esto es suficiente demostrar la unicidad de la representación del
elemento identidad
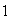 .
Sea
.
Sea
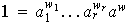 con
con

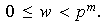
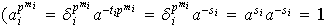
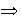
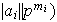
Mediante el homomorfismo canónico
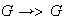
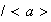 obtenemos
obtenemos
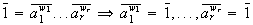 ya que
ya que
 y
y
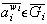 ,
,
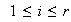

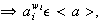
 ,
,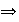
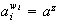 con
con
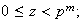
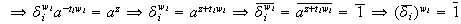 .
Como
.
Como
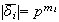 y
y
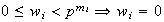 ,
,
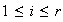
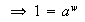 .
Como
.
Como
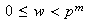

 y
y
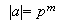
 \
\
El Teorema 2 ha probado que cada grupo abeliano finito de orden
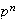 se descompone en suma directa de subgrupos cíclicos
se descompone en suma directa de subgrupos cíclicos

donde
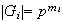 ,
,
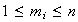 ,
,
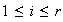 ,
,
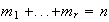 ,
,
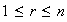 .
(Notese que aquí se ha incluido el caso trivial en el que
.
(Notese que aquí se ha incluido el caso trivial en el que
 es cíclico y
es cíclico y
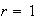 ).
).
Vale la pena entonces preguntar sobre la unicidad de la descomposición anterior.
Teorema 3. Si el grupo abeliano finito G se descompone en dos formas en producto de subgrupos cíclicos
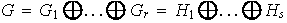
entonces
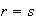 y los órdenes
y los órdenes
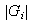 coinciden con los órdenes
coinciden con los órdenes
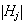 después de una reordenación de índices.
después de una reordenación de índices.