| Lección 2. |
Sistema de Invariantes
|
Según el Teorema 2 cada
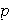 -grupo
abeliano finito
-grupo
abeliano finito
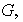
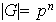 ,
determina una
,
determina una
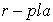
 conformada por los órdenes de los subgrupos cíclicos de su
descomposición:
conformada por los órdenes de los subgrupos cíclicos de su
descomposición:

La suma directa se puede reordenar de tal forma que
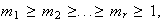
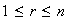 (se ha incluido el caso trivial cuando
(se ha incluido el caso trivial cuando
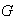 es cíclico y
es cíclico y
 ).
Según el Teorema 3, la longuitud
).
Según el Teorema 3, la longuitud
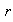 de la
de la
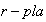 así como sus componentes
así como sus componentes
 ,
están determinadas unívocamente por el grupo
,
están determinadas unívocamente por el grupo
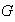 .
Esta primera observación permite dar la siguiente definición.
.
Esta primera observación permite dar la siguiente definición.
Definición 1. Sea
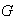 un
un
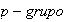 abeliano finito,
abeliano finito,
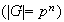 ,
se dice que
,
se dice que
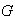 es del tipo
es del tipo
 si
si
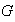 es suma directa de subgrupos
es suma directa de subgrupos
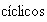 de órdenes
de órdenes
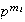 ,
,
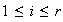 ,
,
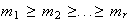 ,
,
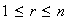 ,
,
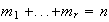 ,
los componentes
,
los componentes
 de la
de la
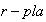 se denominan invariantes (o divisores elementales) del grupo
se denominan invariantes (o divisores elementales) del grupo
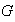 .
.
2) Sean A y B dos
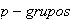 abelianos finitos con el mismo sistema de invariantes
abelianos finitos con el mismo sistema de invariantes
 .
Entonces
.
Entonces
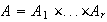 ,
,
 y ademas
y ademas
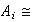
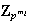
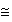
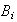 .
Por lo tanto
.
Por lo tanto
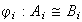 ,
,
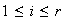 .
El sistema de isomorfismos
.
El sistema de isomorfismos
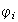 induce
el isomorfismo
induce
el isomorfismo

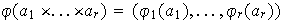
Hemos probado entonces la siguiente proposición .
Proposición 2. Con sus invariantes cada
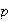 -grupo
abeliano finito se determina unívocamente salvo isomorfismo.
-grupo
abeliano finito se determina unívocamente salvo isomorfismo.
Veamos en un ejemplo la ilustración de los resultados anteriores.
Ejemplo 2. Sea
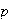 un primo cualquiera y
un primo cualquiera y
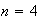 .
Determinemos todos los posibles grupos abelianos de orden
.
Determinemos todos los posibles grupos abelianos de orden
 .
.
Factores invariantes:
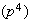 ,
,
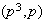 ,
,
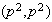 ,
,
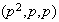 ,
,
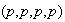 .
Estos tipos determinan salvo isomorfismo únicamente los siguientes grupos
distintos:
.
Estos tipos determinan salvo isomorfismo únicamente los siguientes grupos
distintos:
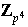 ,
,

 ,
,
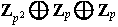 ,
,

El ejemplo anterior permite la siguiente generalización:
Definición 2. Sea
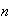 un entero positivo. Una sucesión de enteros positivos
un entero positivo. Una sucesión de enteros positivos
 con
con
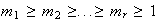 y
y
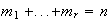 se denomina una partición de
se denomina una partición de
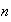 .
Sea
.
Sea
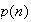 el número de particiones de
el número de particiones de
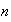 .
.
Ejemplo 3.
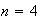 :
:
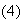 ,
,
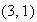 ,
,
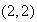 ,
,
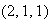 ,
,


Proposición 3. Sea
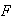 la clase de todos los subgrupos abelianos no isomorfos de orden
la clase de todos los subgrupos abelianos no isomorfos de orden
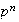 ,
,
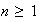 ,
y sea
,
y sea
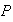 el conjunto de todas las particiones de
el conjunto de todas las particiones de
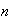 .
Existe una correspondencia
.
Existe una correspondencia
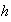 biunívoca entre
biunívoca entre
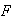 y
y
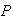 ,
es decir, el número de grupos abelianos no isomorfos de orden
,
es decir, el número de grupos abelianos no isomorfos de orden
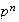 es finito e igual a
es finito e igual a
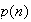 .
.
Demostración. Según el
Teorema 3, cada elemento
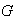 de
de
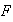 determina unívocamente su tipo
determina unívocamente su tipo
 con
con
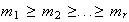 y
y
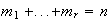 .
Tenemos pues la función
.
Tenemos pues la función
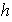 :
:
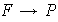
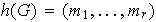
Según la Proposición 2 cada partición
 determina un único grupo (salvo isomorfismo) con sistema de invariantes
determina un único grupo (salvo isomorfismo) con sistema de invariantes
 .
Así pues,
.
Así pues,
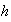 es
es
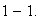 Ahora,
Ahora,
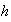 es claramente sobre:
es claramente sobre:
 determina
determina
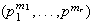 el cual una vez determina
el cual una vez determina
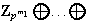
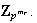 \
\
Ejemplo 4.
1) Determinar todos los subgrupos abelianos de orden
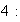
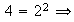
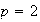 ,
,
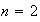
 ,
,
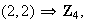
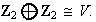
2) Determinar todos los grupos abelianos de orden
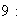
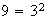 ;
;
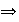
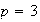 ,
,
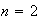
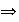
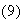 ,
,
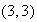
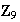 ,
,
 .
.
3) Determinr todos los grupos abelianos de orden
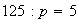 ,
,
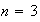
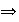
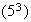 ,
,
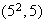 ,
,
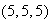
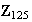 ,
,
 ,
,
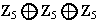 .
.
Definición 3. Un grupo
abeliano de orden
 con sistema de invariantes
con sistema de invariantes
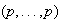 (e.d isomorfo a
(e.d isomorfo a
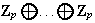 )
se denomina grupo abeliano elemental.
)
se denomina grupo abeliano elemental.