| Lección 3. |
Grupos Abelianos Finitos
|
De los resultados de las lecciones anteriores obtenemos las siguientes conclusiones.
Teorema 4. Cada grupo abeliano finito es suma
directa de
 -subgrupos
cíclicos. Dos descomposiciones difieren sólo en el orden de
disposición de los sumandos.
-subgrupos
cíclicos. Dos descomposiciones difieren sólo en el orden de
disposición de los sumandos.
Demostración. Sea
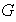 un grupo abeliano finito de orden
un grupo abeliano finito de orden
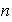
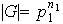 ...
...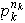 ,
,
 son primos diferentes.
son primos diferentes.
Entonces, según el Teorema 1
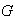 tiene una descomposicion única en suma directa de sus subgrupos de Sylow
(sus componentes primarias!).
tiene una descomposicion única en suma directa de sus subgrupos de Sylow
(sus componentes primarias!).

Según el Teorema 2 cada componente primaria
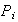 ,
,
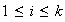 ,
se descompone en suma directa de subgrupos cíclicos (componetes primarias
,
se descompone en suma directa de subgrupos cíclicos (componetes primarias
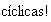 ).
Además, según el Teorema 3 cada
componente primaria
).
Además, según el Teorema 3 cada
componente primaria
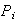 determina unívocamente el número y orden de sus subgrupos
cíclicos:
determina unívocamente el número y orden de sus subgrupos
cíclicos:
 |
 |
. . . . . . . . . . .
 |
donde los
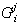 son
son
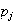 -subgrupos
cíclicos. Entonces,
-subgrupos
cíclicos. Entonces,

Si
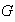 tiene otra descomposicion en suma directa de subgrupos primarios cíclicos
tiene otra descomposicion en suma directa de subgrupos primarios cíclicos
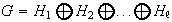 ,
entonces podemos ordenar dichos sumandos de tal forma que colocamos todos los
,
entonces podemos ordenar dichos sumandos de tal forma que colocamos todos los
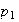 -grupos
a la izquierda, los
-grupos
a la izquierda, los
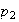 -grupos
a la derecha a continuación y así sucesivamente. Según el
primer Teorema de Sylow en esta nueva descomposicion de
-grupos
a la derecha a continuación y así sucesivamente. Según el
primer Teorema de Sylow en esta nueva descomposicion de
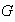 deben aparecer
deben aparecer
 grupos para cada primo
grupos para cada primo
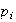 ,
,
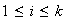 .
.
Además, según el segundo Teorema de Sylow los
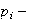 sumandos
conforman el
sumandos
conforman el
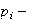 subgrupo
de Sylow de
subgrupo
de Sylow de
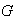 .
Luego según el Teorema 3, los
.
Luego según el Teorema 3, los
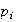 sumandos de la nueva descomposicion deben ser tantos como
sumandos de la nueva descomposicion deben ser tantos como
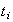 ,
,
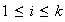 ,
además los órdenes deben coincidir con los órdenes de
,
además los órdenes deben coincidir con los órdenes de
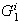 ,...,
,...,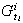 .▫
.▫
El teorema anterior describe pues de manera completa los grupos abelianos finitos en términos de grupos primarios cíclicos.
Corolario 2. El número de grupos abelianos no isomórficos de orden
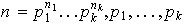 primos diferentes
primos diferentes
es
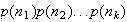 ,
donde
,
donde
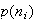 es el número de particiones del entero positivo
es el número de particiones del entero positivo
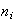 ,
,
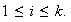
Demostración. Consecuencia directa del teorema anterior y de la Proposición 3.▫
Proposición 4. (Recíproco del Teorema de
Lagrange para grupos abelianos finitos) Sea
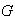 un grupo abeliano finito y sea
un grupo abeliano finito y sea
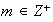 tal que
tal que
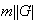 .
Entonces
.
Entonces
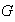 contiene al menos un subgrupo de orden
contiene al menos un subgrupo de orden
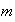 .
.
Demostración. Sea
 y sea
y sea
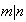 ,
,
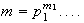
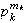 con
con
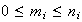 ,
,
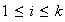
Existen en
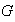 subgrupos
subgrupos
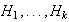 de órdenes
de órdenes
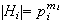 ,
,
 .
Como
.
Como
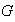 es abeliano
es abeliano
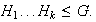 Veamos que
Veamos que
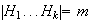 .
Para ello probemos que
.
Para ello probemos que
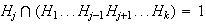 ,
para cada
,
para cada
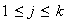 .
.
Sea
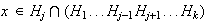 ,
entonces
,
entonces
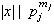 y
y
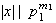 ...
...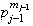
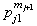 ...
...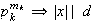 ,
donde
,
donde
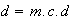
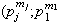 ...
...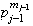
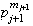 ...
...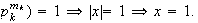
Ejemplo 4. 1) Determinar todos los grupos abelianos de orden 1440.
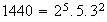 ;
;
p(5): (5),(4,1),(3,2),(3,1,1),(2,2,1),(2,1,1,1),(1,1,1,1,1);
p(1)=(1);
p(2):(2),(1,1);
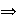
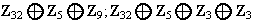
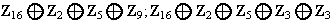
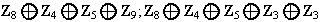
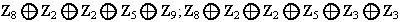

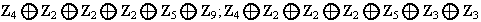 ,
,
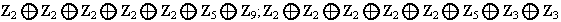
2)Demuestre que
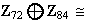
 :
:
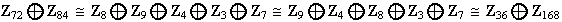
3) Son
 y
y
 isomórfos ?
isomórfos ?

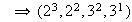 ;
;

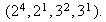
Puesto que los invariantes son diferentes, dichos grupos no son isomórfos.