| Ejercicios |
Ejercicio 13. Demostrar que los subgrupos de
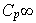 son: 1 =
son: 1 =
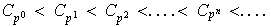
Solución. Sea
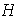 un subgrupo propio de
un subgrupo propio de
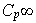 .
Si para cada
.
Si para cada
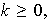
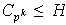 ,
entonces
,
entonces
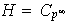 ,
pero este caso está descartado. Entonces existe un
,
pero este caso está descartado. Entonces existe un
 tal que
tal que
 no está incluido en
no está incluido en
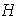 .
Escojamos el menor
.
Escojamos el menor
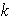 tal que
tal que
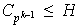 pero
pero
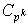 no está incluido en
no está incluido en
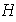 .
.
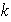 no puede ser
no puede ser
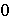 ya que
ya que
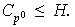 Por lo tanto
Por lo tanto
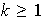 .
La idea es entonces demostrar que
.
La idea es entonces demostrar que
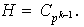 Si esto es así entonces el
Si esto es así entonces el
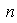 buscado es
buscado es
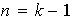 .
.
Sabemos que
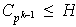 y supongamos que la inclusión es estricta, es decir, existe
y supongamos que la inclusión es estricta, es decir, existe
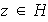 pero
pero
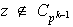 .
Como
.
Como
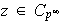 existe un
existe un
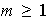
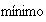 tal que
tal que
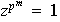 pero
pero
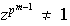 .
Nótese que
.
Nótese que
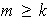 porque de lo contario
porque de lo contario
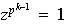 y así
y así
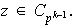 Se tiene que
Se tiene que
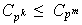 .
Sea
.
Sea
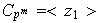 ,
entonces
,
entonces
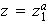 ,
donde
,
donde
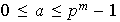 ,
nótese que
,
nótese que
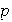 no divide al entero
no divide al entero
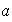 .
En efecto, si
.
En efecto, si
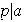 ,
entonces
,
entonces
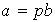 y entonces
y entonces
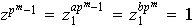 ,
pero esto indica que
,
pero esto indica que
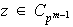 ,
lo cual es falso. Se tiene entonces que
,
lo cual es falso. Se tiene entonces que
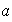 y
y
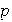 son primos realtivos, es decir,
son primos realtivos, es decir,
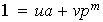 ,
donde
,
donde
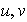 son enteros. De aquí resulta que
son enteros. De aquí resulta que
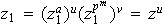 .
Esto implica que
.
Esto implica que
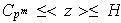 y de aquí se tendría que
y de aquí se tendría que
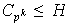 ,
lo cual es falso. En conclusión,
,
lo cual es falso. En conclusión,
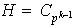 .\
.\