| Ejercicios |
Ejercicio 1. Sea
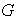un grupo,
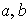elementos de
tales que:
i)
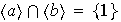
ii)
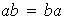
iii)
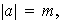
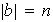
Entonces,
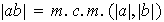
Ejercicio 2. Sea
un grupo,
elementos de
tales que:
i)
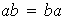
ii)
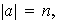
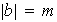
iii)
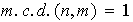
Entonces,
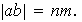Además,
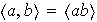
Ejercicio 3. Sea
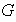un grupo y sean
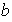elementos de
.
Entonces:
i)
ii)
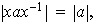para todo
.
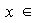
iii)
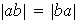
iv) Sea
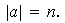Entonces, (
)
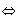
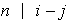Ejercicio 4. Sea
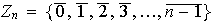el conjunto de los enteros módulo
.
En
definimos la multiplicación mediante la regla:
.
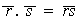Demostrar que
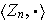es un semigrupo conmutativo con elemento identidad
( Compruebe inicialmente que la operación
en
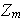está bien definida! ). Construya la tabla para
.
Es
un grupo?
Ejercicio 5. Sea
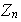el conjunto de los enteros módulo
.
Sea
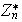el grupo multiplicativo del semigrupo
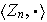del ejercicio anterior. Demostrar que:
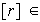
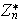
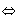
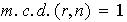
Ejercicio 6. La función
del conjunto de los números naturales que asigna a cada natural
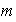el número de enteros positivos menores que
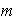y que son primos relativos con él. Por ejemplo,
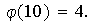La función
es denominada función de Euler. Según el ejercicio anterior,
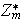tiene
elementos. Utilizar estas observaciones para demostrar los siguientes
teoremas:
i) Teorema de Euler: Sean
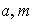enteros,
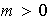y
.
Entonces
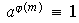(módulo
),
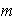es decir,
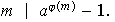
ii) Teorema de Fermat: Si
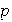es primo entonces
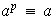(módulo
),
para todo
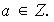
Ejercicio 7. Sea
un grupo cíclico de orden
.
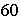Cuántos generadores tiene
?
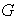Ejercicio 8. Determinar el subgrupo cíclico
de
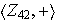generado por
Ejercicio 9. Demostrar que
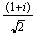es un elemento de período finito de
.
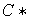Ejercicio 10. Sean
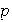y
primos diferentes. Encontrar el número de generadores del grupo
cíclico
Ejercicio 11. Determinar todos los subgrupos de
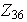y todos sus generadores.
Ejercicio 12. Determinar todos los subgrupos de
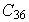y todos sus generadores.
Ejercicio 13.
Demostrar que los subgrupos de
son: 1 =
