| Lección 5. |
Teorema
|
Teorema 1. i) Sea
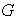 un grupo cíclico finito de orden
un grupo cíclico finito de orden
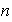 con generador
con generador
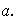 Entonces:
Entonces:
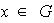 es generador de
es generador de
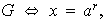 donde
donde
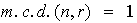
ii) Sea
 un grupo cíclico con generador
un grupo cíclico con generador
 y sea
y sea
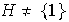 un subgrupo de
un subgrupo de
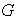 .
Entonces
.
Entonces
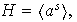 donde
donde
 es el menor entero positivo tal que
es el menor entero positivo tal que
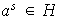 .
Además, si
.
Además, si
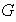 es de orden finito
es de orden finito
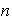 entonces
entonces
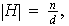
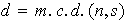
iii) Sea
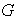 un grupo cíclico de orden finito
un grupo cíclico de orden finito
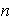 y sea
y sea
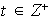 tal que
tal que
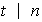 .
Entonces
.
Entonces
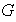 contiene exactamente un subgrupo de orden
contiene exactamente un subgrupo de orden
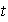 .
.
Demostración. i)
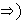 Sea
Sea
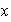 un generador de
un generador de
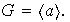 Entonces existe un
Entonces existe un
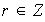 tal que
tal que
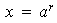 y
y
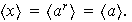 De aquí obtenemos que
De aquí obtenemos que
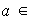
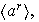 es decir existe
es decir existe
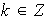 tal que
tal que
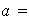
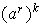 entonces
entonces
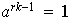 ,
así
,
así
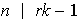 es decir
es decir
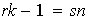 ,
con
,
con
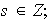 de lo cual
de lo cual
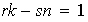 ,
así
,
así
 y
y
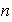 son primos relativos y
son primos relativos y
 .
.
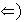 Sea
Sea
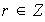 tal que
tal que
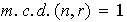 .
Lógicamente,
.
Lógicamente,
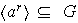 .
Sea
.
Sea
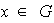 ,
entonces existe
,
entonces existe
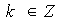 tal
que
tal
que Como
Como
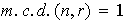 existen
existen
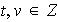 tales que
tales que
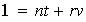 ,
así
,
así
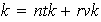 ;
luego
;
luego
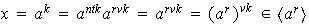
ii) La primera parte de esta afirmación fue demostrada en el punto ii) de la Proposición 2.
Para la segunda parte, el orden de
 es el orden de
es el orden de
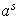 .
Sea
.
Sea
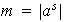 ,
entonces
,
entonces
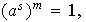 es decir,
es decir,
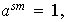 luego
luego
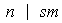 ,
por lo tanto
,
por lo tanto
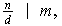 siendo
siendo
 .
De otra parte,
.
De otra parte,
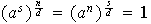 entonces
entonces
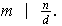 Por lo tanto,
Por lo tanto,
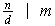 y
y
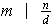 con lo cual
con lo cual
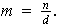
iii) Existencia: como
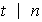 entonces
entonces
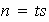 ,
con
,
con
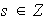 ,
así
,
así
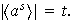 En efecto,
En efecto,
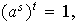 entonces
entonces
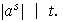 Si
Si
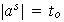 y
y
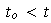 entonces
entonces
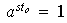 y
y
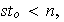 lo cual es una contradicción.
lo cual es una contradicción.
Unicidad: sea
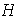 un subgrupo de
un subgrupo de
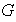 de orden
de orden
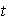 .
Sea
.
Sea
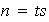 y sea
y sea
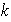 el menor entero positivo tal que
el menor entero positivo tal que
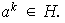 Por ii) sabemos que
Por ii) sabemos que
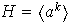 y
y
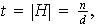 donde
donde
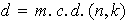 ;
entonces
;
entonces
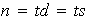 de modo que
de modo que
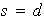 ,
así
,
así
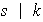 ,
es decir,
,
es decir,
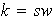 con
con
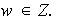 Luego,
Luego,
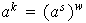 y por tanto
y por tanto
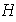
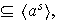 pero
pero
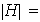
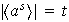 entonces
entonces
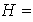
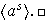
Ejemplo 2: los enteros módulo n Sea
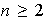 un entero, entonces el conjunto
un entero, entonces el conjunto
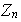 conformado por todos los enteros
conformado por todos los enteros
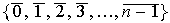 conforman un grupo
conforman un grupo
 respecto de la siguiente adición:
respecto de la siguiente adición:
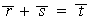 , donde
, donde
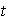 es el resíduo de dividir
es el resíduo de dividir
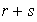 entre
entre
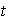 .
Nótese que el generador de
.
Nótese que el generador de
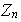 es
es
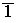 .
El grupo
.
El grupo
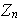 lo consideraremos nuevamente en el Capítulo 5. Por ahora digamos algo
más respecto a su definición. También podríamos haberlo
definido usando las ideas previas al teorema de Lagrnage, es decir, se
vió que en
lo consideraremos nuevamente en el Capítulo 5. Por ahora digamos algo
más respecto a su definición. También podríamos haberlo
definido usando las ideas previas al teorema de Lagrnage, es decir, se
vió que en
 se puede definir la relación de equivalencia
se puede definir la relación de equivalencia
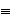 respecto del subgrupo
respecto del subgrupo
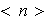 en la forma
en la forma
 si y sólo si
si y sólo si
 .
Esta relación divide a
.
Esta relación divide a
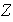 en
en
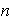 clases de equivalencia de la forma
clases de equivalencia de la forma
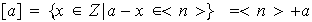 .
Las clases en este caso se denotan mejor en la forma
.
Las clases en este caso se denotan mejor en la forma
![$[a]=\overline{a}$](graphics/cap2s4__118.png) ,
y la suma de clases se hace como se dijo arriba. Nótese que las clase
distintas son exactamente
,
y la suma de clases se hace como se dijo arriba. Nótese que las clase
distintas son exactamente
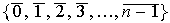 .
Qeremos ahora calcular todos los subgrupos de
.
Qeremos ahora calcular todos los subgrupos de
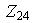 y todos sus generadores.
y todos sus generadores.
Si
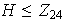 entonces
entonces
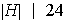 de modo que
de modo que
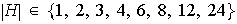
Para
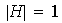 tenemos
tenemos
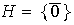 y para
y para
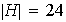 tenemos
tenemos
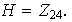
Para cada
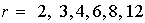 sabemos que
sabemos que
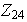 contiene solamente un subgrupo de orden
contiene solamente un subgrupo de orden
 .
Ahora, cada subgrupo H es cíclico y de la forma
.
Ahora, cada subgrupo H es cíclico y de la forma
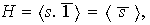 donde
donde
 siendo
siendo 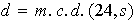 .
Obtenemos pues:
.
Obtenemos pues:
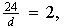 entonces
entonces
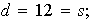
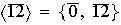
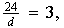 entonces
entonces
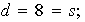

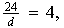 entonces
entonces
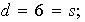
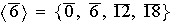
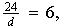 entonces
entonces
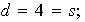

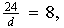 entonces
entonces
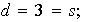
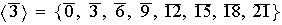
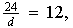 entonces
entonces
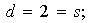
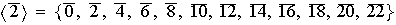
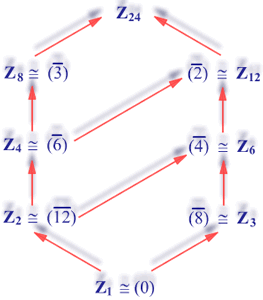
Los generadores de
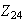 son de la forma
s.
son de la forma
s.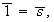 con
con
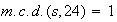 .
Entonces
.
Entonces
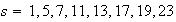 .
El símbolo
.
El símbolo
 en el diagrama anterior indica isomorfismo y será explicado más
adelante.
en el diagrama anterior indica isomorfismo y será explicado más
adelante.