| Lección 4. |
Propiedadesn
|
Las siguientes afirmaciones son válidas para grupos cíclicos cualesquiera. Especialmente importante es la afirmación iv).
Proposición 2. i) Todo grupo cíclico es abeliano.
ii) Cada subgrupo de un grupo cíclico es cíclico.
iii) Si
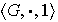 es un grupo cíclico infinito entonces cada subgrupo de
es un grupo cíclico infinito entonces cada subgrupo de
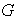 diferente de
diferente de
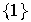 es también infinito.
es también infinito.
iv) Sea
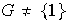 un grupo. Entonces G es un grupo cíclico finito de orden primo si y
sólo si G no tiene subgrupos diferentes de los triviales.
un grupo. Entonces G es un grupo cíclico finito de orden primo si y
sólo si G no tiene subgrupos diferentes de los triviales.
Demostración.
i) Esta propiedad se deduce de la regla de exponentes
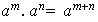 válida en todo grupo.
válida en todo grupo.
ii) Sea
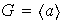 un grupo cíclico generado por el elemento
un grupo cíclico generado por el elemento
 Sea
Sea
 un subgrupo de
un subgrupo de
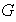 .
Si
.
Si
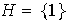 entonces él es claramente cíclico con generador 1. Sea
entonces él es claramente cíclico con generador 1. Sea
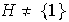 ,
entonces existe un
,
entonces existe un
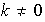 tal que
tal que
 .
Esto indica que
.
Esto indica que
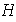 contiene potencias enteras positivas del elemento
contiene potencias enteras positivas del elemento
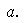 Por el principio de buena ordenación del conjunto
Por el principio de buena ordenación del conjunto
 escogemos el menor entero positivo
escogemos el menor entero positivo
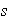 tal que
tal que
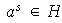 .
Afirmamos que
.
Afirmamos que
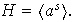 Claramente
Claramente
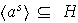 .
Sea
.
Sea
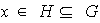 ,
entonces existe
,
entonces existe
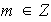 tal que
tal que
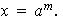 Utilizando el algoritmo de la división encontramos enteros
Utilizando el algoritmo de la división encontramos enteros
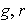 tales que
tales que
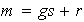 ,
con
,
con
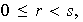 entonces
entonces
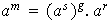 de donde
de donde
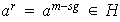 .
Por la elección de
.
Por la elección de
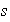 concluimos que
concluimos que
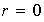 y así
y así
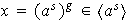
iii) Sea
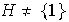 un subgrupo del grupo cíclico infinito
un subgrupo del grupo cíclico infinito
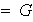 .
Según ii) existe
.
Según ii) existe
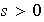 tal que
tal que
 .
Si
.
Si
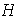 es finito entonces eso quiere decir que el orden de
es finito entonces eso quiere decir que el orden de
 es finito con lo cual
es finito con lo cual
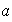 es de período finito y así
es de período finito y así
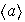 es finito, lo cual contradice la hipótesis. Esto indica que
es finito, lo cual contradice la hipótesis. Esto indica que
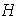 debe ser infinito.
debe ser infinito.
iv)
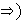 Sea
Sea
 un grupo finito de orden primo
un grupo finito de orden primo
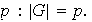 Sea
Sea
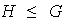 ,
entonces
,
entonces
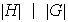 de modo que
de modo que
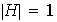 ó
ó
 por lo tanto
por lo tanto
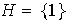 ó
ó
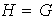 .
.
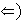 Sea
Sea
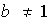 ,
,
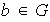 .
El subgrupo cíclico
.
El subgrupo cíclico
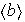 generado por b es entonces diferente de
generado por b es entonces diferente de
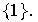 Por lo tanto
Por lo tanto
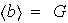 ,
esto quiere decir que G es
,
esto quiere decir que G es
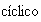 .
Probemos ahora que G es finito. Consideremos el subgrupo cíclico
generado por
.
Probemos ahora que G es finito. Consideremos el subgrupo cíclico
generado por
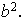 Por la condición de la hipótesis
Por la condición de la hipótesis
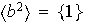 ó
ó
 .
En el primer caso tendremos que
.
En el primer caso tendremos que
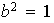 con lo cual
con lo cual
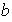 es de período 1 ó 2. No puede ser de período 1 ya que
es de período 1 ó 2. No puede ser de período 1 ya que
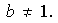 Por lo tanto
Por lo tanto
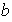 es de período 2 y así
es de período 2 y así
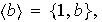 con lo cual, G es finito y su orden es el primo 2. Supóngase que
con lo cual, G es finito y su orden es el primo 2. Supóngase que
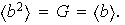 Existe entonces
Existe entonces
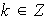 tal que
tal que
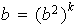 ,
es decir,
,
es decir,
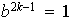 con lo cual
con lo cual
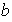 es de período finito y
es de período finito y
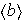 es finito; es decir G es finito. Resta sólo probar que el orden de G
es un numero primo. Sea
es finito; es decir G es finito. Resta sólo probar que el orden de G
es un numero primo. Sea
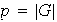 el orden del grupo G y sea
el orden del grupo G y sea
 tal que
tal que
 .
Consideremos el subgrupo cíclico generado por
.
Consideremos el subgrupo cíclico generado por
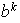 .
Si
.
Si
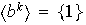 entonces
entonces
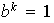 y
y
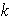 es un múltiplo del período
es un múltiplo del período
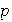 ,
con lo cual
,
con lo cual
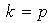 .
Supóngase ahora que
.
Supóngase ahora que
 entonces existe
entonces existe
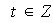 tal que
tal que
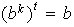 ,
así
,
así
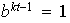 entonces
entonces
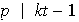 ,
es decir que existe
,
es decir que existe
 tal que
tal que
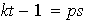 ;
pero
;
pero
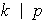 entonces existe
entonces existe
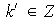 tal que
tal que
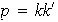 ;
luego
;
luego
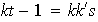 ; así
; así
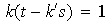 entonces
entonces
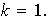 Esto prueba que los únicos divisores de
Esto prueba que los únicos divisores de
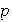 son
son
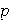 y
y
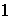 ,
con lo cual
,
con lo cual
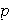 es
primo.
es
primo.