| Lección 1. |
Subgrupo Normal
|
En el Capítulo I fue construido el grupo de enteros módulo
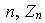 ,
por medio de 4 objetos, a saber: el grupo
,
por medio de 4 objetos, a saber: el grupo
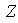 ,
el subgrupo
,
el subgrupo
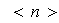 de
de
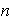 ,
la relación de equivalencia en
,
la relación de equivalencia en
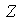 definida como
definida como
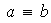 si y sólo si
si y sólo si
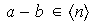 y la operación de adición entre clases de equivalencia determinadas
por esta relación:
y la operación de adición entre clases de equivalencia determinadas
por esta relación:
 ,
,
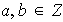
Vale la pena preguntarnos si, dado un grupo
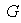 y
y
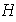 un subgrupo cualquiera de
un subgrupo cualquiera de
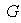 ,
podemos repetir la construcción mencionada anteriormente con ayuda de la
relación de equivalencia en
,
podemos repetir la construcción mencionada anteriormente con ayuda de la
relación de equivalencia en
 utilizada para la demostración del Teorema de Lagrange:
utilizada para la demostración del Teorema de Lagrange:
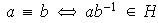 .
Puesto que las clases de equivalencia están determinadas por el subgrupo
.
Puesto que las clases de equivalencia están determinadas por el subgrupo
 ,
será lógico preguntarnos que condición debe satisfacer
,
será lógico preguntarnos que condición debe satisfacer
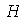 para que podamos dar al conjunto de clases de equivalencia una estructura de
grupo. Antes de responder a estas preguntas recordemos cierta
terminología ya introducida antes por nosotros.
para que podamos dar al conjunto de clases de equivalencia una estructura de
grupo. Antes de responder a estas preguntas recordemos cierta
terminología ya introducida antes por nosotros.
Definición 1. Sea
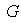 un grupo y sean
un grupo y sean
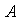 y
y
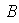 subconjuntos no vacíos de
subconjuntos no vacíos de
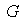 ,
se denomina producto de los conjuntos
,
se denomina producto de los conjuntos
 y
y
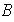 (en ese orden) al conjunto de productos de la forma
(en ese orden) al conjunto de productos de la forma
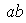 ,
donde
,
donde
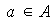 y
y
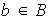 ,
y se denota por
,
y se denota por
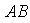 .
En otras palabras,
.
En otras palabras,
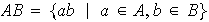 .
.
Proposición 1. Sea
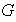 un grupo y sea
un grupo y sea
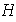 un subgrupo de
un subgrupo de
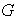 .
Entonces las siguientes condiciones son equivalentes:
.
Entonces las siguientes condiciones son equivalentes:
1)
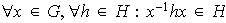
2)
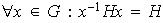
3)
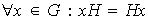
4)
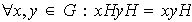
Demostración.
1)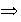 2)
Evidentemente
2)
Evidentemente
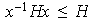 .
Sea ahora
.
Sea ahora
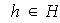 .
Entonces
.
Entonces
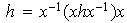 ; según 1)
; según 1)
 ;
así pues,
;
así pues,
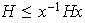 .
.
2)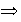 3):
Sea
3):
Sea
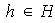 ,
entonces
,
entonces
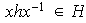
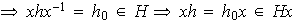 ;
;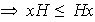 Análogamente,
Análogamente,
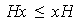 .
.
3)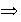 4):
Sean
4):
Sean
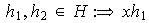
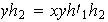 donde
donde
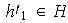 ;
;
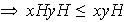 .
Ahora, si
.
Ahora, si
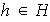 se obtiene que
se obtiene que
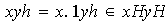 ,
es decir,
,
es decir,
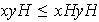 .
.
4)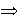 1):
Sea
1):
Sea
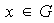 ,
,
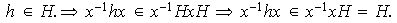
Esto completa la prueba de la
proposición.
Definición 2. Sea
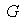 un grupo y
un grupo y
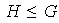 .
Se dice que
.
Se dice que
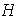 es un subgrupo normal de
es un subgrupo normal de
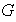 , lo cual denotamos por
, lo cual denotamos por
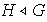 ,
si
,
si
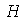 cumple una de las condiciones de la proposicion anterior.
cumple una de las condiciones de la proposicion anterior.
Definición 3. Sea
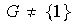 un grupo. Entonces
un grupo. Entonces
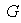 posee al menos dos subgrupos normales, llamados los subgrupos normales
triviales:
posee al menos dos subgrupos normales, llamados los subgrupos normales
triviales:
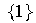 ,
,
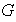 .
Si
.
Si
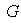 no posee otros subgrupos normales fuera de los triviales se dice que
no posee otros subgrupos normales fuera de los triviales se dice que
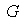 es un grupo simple.
es un grupo simple.