| Lección 4. |
Homomorfismo de Grupos - Concepto
|
En esta lección se ilustra el importante concepto de homomorfismo de grupos así como también algunas de las propiedades fundamentales de estas funciones. Al final, con ayuda del concepto de isomorfismo se hace una clasificación de los grupos cíclicos.
Definición 4. Sea
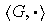y
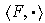dos
grupos
Una función
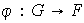
tal que:
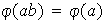
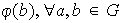
se denomina un homomorfissmo del grupo
en el grupo
.
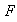Si ambos tienen notación aditiva, entonces la condición anterior se
escribe como
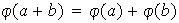
Veamos algunos ejemplos:
1) Sea
el grupo aditivo de los números reales, y sea
el grupo multiplicativo de los números reales no nulos. La función
definida por
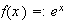es un homomorfismo de
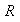en
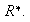
2) Homomorfismo nulo: sea
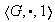un grupo multiplicativo y sea
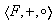un grupo con notación aditiva. La función de
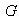en
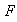definda por:
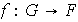
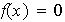
es un homomorfismo, Además la función
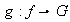es definida por
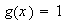es también un homomorfismo; lo podemos denominar homomorfismo unitario.
3) Homomorfismo idéntico: sea
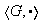un grupo. La función
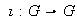de
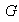en si mismo definida por
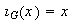es un homomorfismo.
Definición 5. Sea
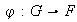un homomorfismo de grupos.
1) Sea
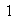el elemento identidad del grupo
.
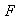El conjunto de elementos de
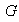cuya imagen es el elemento identidad
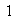de
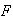se denomina el núcleo de
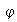y se denota por
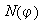o tambíén por
:
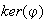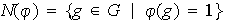
2) Sea
.
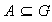El conjunto de las imágenes de los elementos del
conjunto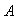 
se denomina imagen del conjunto
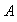mediante
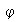y se denota por
:
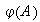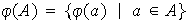
En particular el conjunto
se denomina la imagen del homomorfismo
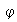y se simboliza también por
.
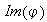3) Sea
.
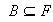El conjunto de elementos de
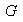cuyas imágenes pertenencen al conjunto
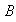se denomina imagen inversa de
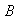mediante
y se simboliza por
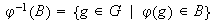
4) Se dice que
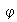es un homomorfismo inyectivo si
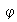es una función inyectiva, es decir, para cualesquiera elementos
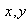
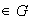se cumple la implicación:
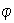
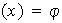
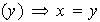
5) Se deice que
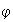es un homomorfismo sobreyectivo si
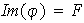
6) Se dice que
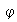es un isomorfismo o también que
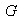y
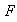son isomórficos, lo cual simbolizamos por
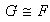si
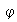
es inyectivo y sobreyectivo simultáneamente.
Proposición 4. Sea
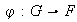un homomorfismo, entonces:
1)
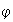
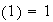
2)
,
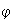
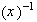para cada
.
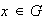3)
.
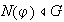4) La imagen de un subgrupo de
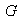mediante
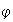es un subgrupo de
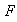es decir:
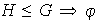
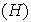
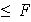
5) La imagen inversa de un subgrupo de
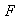mediante
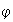es un subgrupo de
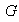es decir:
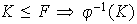
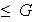
6) La imagen de un subgrupo normal de
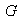mediante
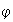es un subgrupo normal de la imagen de
,
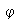es decir:
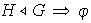
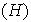
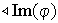
7) La imagen inversa de un subgrupo normal de
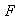mediante
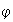es un subgrupo normal de
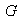es decir:
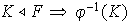
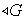
8)
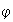es inyectivo
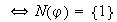
9) Sea
.
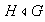La función
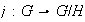definida por
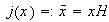es un homomorfismo sobreyectivo.
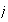se denomina el homomorfismo cónico
10)
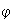es un isomorfismo si y sólo si existe una función
,
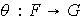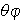
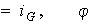
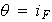
Además,
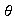es también un homomorfismo.
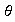se denomina el homomorfismo inverso de
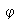y se denota por
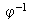
11) Sea
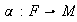un homomorfismo. Entonces la función compuesta
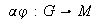es un homomorfismo.
Demostración. Todas las pruebas se reducen a aplicar directamente las definiciones anteriores.▫