| Lección 3. |
Grupo Cociente - Ejercicios
|
Ejercicio 1. Demostrar que en un grupo abeliano todos sus subgrupos son normales
Ejercicio 2. Sea
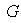 un grupo y
un grupo y
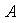 un subconjunto no vacío de
un subconjunto no vacío de
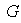 .
Sea
.
Sea
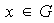 el conjunto:
el conjunto:
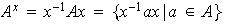
se denomina el conjugado de
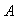 por
por
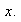
De mostrar que el conjugado de un subgrupo de
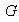 mediante cualquier elemento
mediante cualquier elemento
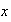 de
de
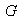 es también un subgrupo de
es también un subgrupo de
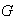 .
.
Demostrar que siendo
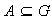 ,
,
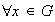 ,
,
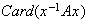
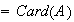
Ejercicio 3. Sea
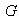 un grupo,
un grupo,
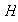 un subgrupo de
un subgrupo de
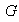 y
y
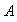 un subconjunto no vacío de
un subconjunto no vacío de
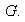 Demostrar que:
Demostrar que:
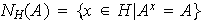 y
y
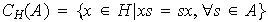
son subgrupos de
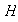 (
(
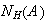 se llama el normalizador de
se llama el normalizador de
 en
en
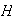 y
y 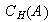 se llama el centralizador de
se llama el centralizador de
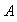 en
en
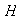 ). Comprobar además que
). Comprobar además que
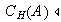
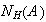 .
.
Ejercicio 4. Sea
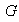 un grupo y
un grupo y
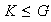 .
Con las definiciones del ejercicio anterior
.
Con las definiciones del ejercicio anterior
 se denomina el normalizador de
se denomina el normalizador de
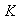 en
en
 y
y
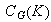 se denomina el centralizador de
se denomina el centralizador de
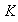 .
El centralizador de
.
El centralizador de
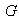 se denota por
se denota por
 y se llama el centro del grupo
y se llama el centro del grupo
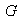 .
Demostrar que :
.
Demostrar que :
i)
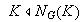 y
y
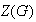 es un grupo abeliano.
es un grupo abeliano.
ii)
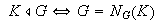
iii) Sea
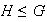 tal que
tal que
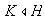 .
Entonces
.
Entonces
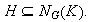
Ejercicio 5.
Sea 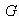 un grupo,
un grupo,
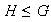 ,
,
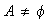 ,
,
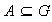 .
Denotemos por
.
Denotemos por
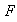 a la familia de subconjuntos de
a la familia de subconjuntos de
 constituidos por los conjugados de
constituidos por los conjugados de
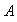 con elementos de
con elementos de
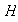 ,
es decir
,
es decir
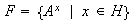 .
Demostrar que
.
Demostrar que
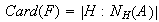
Ejercicio 6. Demostrar que la intersección
de dos subgrupos normales es un subgrupo normal. Generalizar este resultado a
una familia no
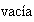 cualquiera de subgrupos normales.
cualquiera de subgrupos normales.
Ejercicio 7. Sea
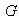 un grupo y
un grupo y
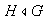 .
Demostrar que las relaciones de equivalencia
.
Demostrar que las relaciones de equivalencia
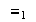 y
y
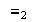 definidas por
definidas por
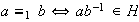 y
y
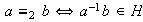 son iguales, es decir
son iguales, es decir