| Lección 1. |
Teorema Fundamental
|
Se mostrará en esta lección que un grupo
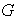tiene tantas imágenes homomórficas como grupos cocientes por
subgrupos normales, este es precisamente el contenido del teorema fundamental
de homomorfismo.
Teorema 1. Sea
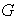un grupo cualquiera. Entonces hay tantas imágenes homomórficas de
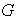como subgrupos normales tiene
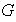(o lo que es lo mismo, como grupos cocientes de
).
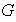Más exactamente: si
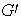es una imagen homomórfica de
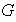entonces existe un subgrupo normal
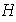de
tal que
.
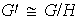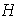es precisamente el núcleo del homomorfismo
.
Recíprocamente, dado un subgrupo normal
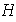de
,
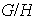es una imagen homomórfica de
.
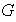El homomorfismo sobreyectivo requerido es el homomorfismo canónico
.
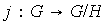Demostración. Sea
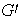una imagen homomórfica de
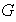con homomorfismo sobreyectivo
:
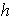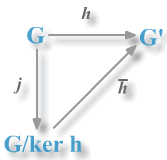
Sea
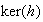el núcleo de
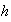y sea
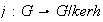el homomorfismo canónico de
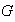sobre el grupo cociente
.
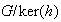Se define la función
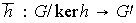
mediante
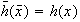, donde
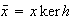es la clase de equivalencia (clase lateral izquierda) determinada por el
elemento
.
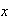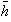está bien definida,
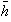es sobre y
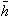es inyectiva. Además,
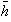es un homomorfismo de grupos. Finalmente, ya se ha visto que la función
canónica
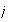es un homomorfismo sobre de
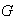en
.\
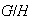Corolario 1. Sea
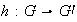un homomorfismo de grupos. Entonces
.
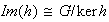Ejemplo 1. 1) Determinar todas las imágenes
homomórficas del grupo aditivo de los números enteros
:
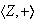según el teorema fundamental de homomorfismo las imágenes
homomórficas de
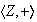son los subgrupos cociente de
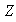por sus subgrupos normales. De esta manera debemos determinar todos los
subgrupos normales
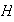de
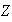y construir los grupos cociente
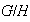. Como
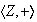es un grupo abeliano entonces cada uno de sus subgrupos es normal. Así
pues, las imágenes homomórficas de
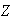son de la forma
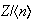con
,
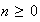es decir las imágenes de
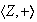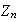son
con
.
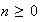2) Sea
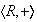el grupo de los números reales bajo la adición y sea
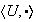el grupo multiplicativo de los complejos de módulo 1:
.
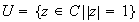Nótese que
.
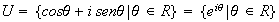La función
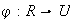definida por
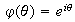es un homomorfismo: en efecto,
.
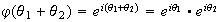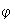es obviamente un homomorfismo sobreyectivo ya que cada complejo tiene
determinado al menos un argumento
. Según el teorema fundamental de homomorfismo
;
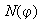
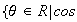
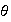
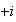
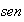
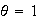
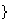
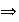si
,
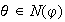
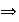
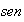
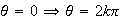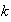
Z . Recíprocamente, cada real de forma
,
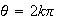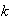
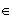
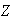es un elemento de
,
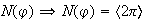grupo generado por
,
.
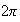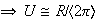3) Imágenes homomórficas de
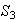: determinamos en primer lugar los subgrupos de
.
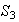Puesto que
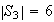entonces
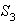sólo puede tener grupos de orden 1,2,3 y 6:
,
;
,
,
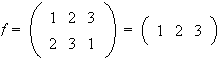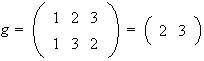
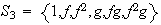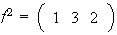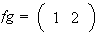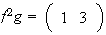
es el único subgrupo de orden 1
Los subgrupos de orden 2 son cíclicos y por lo tanto generados por los elementos de orden 2 :
,
,
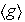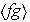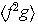son los subgrupos de orden 2
Los subgrupos de orden 3 son necesariamente cíclicos y son generados por elementos de orden 3 :
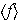es
el único subgrupo de orden 3
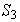es el único subgrupo de orden 6
1 y
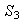son normales. Puesto que
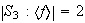entonces
.
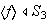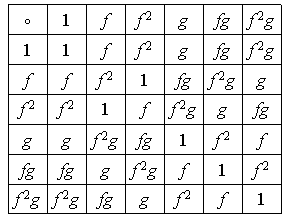
Para la determinación de subgrupos normales de orden 2 no sobra construir
la tabla del grupo
:
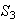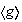no es subgrupo normal de
ya que :
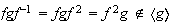
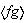no es subgrupo normal de
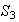ya que :
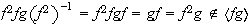
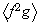no es subgrupo normal de
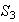ya que :
.
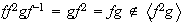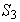no tiene subgrupos normales de orden 2
,
,
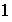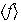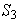son los subgrupos normales de
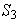
De aquí obtenemos que las imágenes hommórficas de
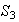(salvo isomorfismos!) son :
,
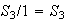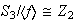ya que :
;
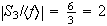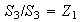(grupo unitario).