| Lección 2. |
Teorema de Factorización
|
Definición 1. Sea
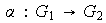 un homomorfismo de grupos. Se dice que el homomorfismo se puede factorizar a
través del homomorfismo
un homomorfismo de grupos. Se dice que el homomorfismo se puede factorizar a
través del homomorfismo
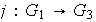 ( o también se dice a través del grupo
( o también se dice a través del grupo
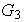 )
)
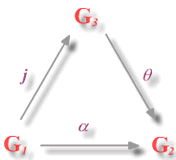
si existe un homomorfismo
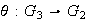 tal que el diagrama anterior conmuta, es decir :
tal que el diagrama anterior conmuta, es decir :
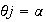 .
.
Teorema 2.
Sea 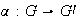 un homomorfismo de grupos y sea
un homomorfismo de grupos y sea
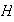 un subgrupo normal de
un subgrupo normal de
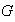 .
Entonces
.
Entonces
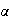 se puede factorizar de una manera
se puede factorizar de una manera
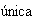 a través de
a través de
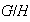 si y sólo
si
si y sólo
si 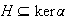 .
.
Demostración.
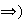 Sea
Sea
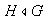 tal que
tal que
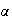 se puede factorizar a través de
se puede factorizar a través de
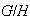 :
:
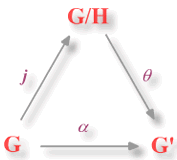
Esto quiere decir que existe un homomorfismo
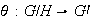 tal que
tal que
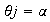 . Sea
. Sea
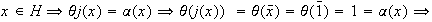
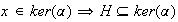 .
.
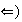 Supóngase que
Supóngase que
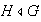 tal que
tal que
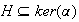 .
Definimos
.
Definimos
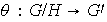
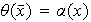 ,
,
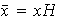 ,
,
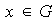 .
.
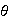 está bien definida :
está bien definida :

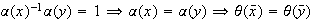 .
.
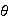 es homomorfismo :
es homomorfismo :
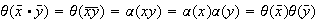 .
.
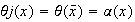 , para todo
, para todo
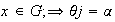 .
.
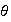 es única : sea
es única : sea
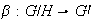 un homomorfismo tal que
un homomorfismo tal que
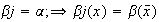
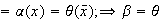 .
.

Corolario 2. 1)
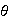 es un homomorfismo inyectivo
es un homomorfismo inyectivo
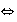
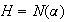 .
Además,
.
Además,
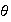 es sobreyectivo
es sobreyectivo
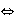
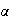 es sobreyectivo.
es sobreyectivo.
2) Cada homomorfismo sobreyectivo
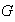 ,,
,,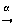 ,,
,,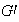 se puede factorizar de manera única a través del grupo factor
se puede factorizar de manera única a través del grupo factor
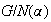 :
:
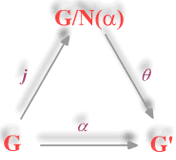
Además en este caso
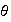 es un isomorfismo
(
es un isomorfismo
(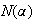 denota el núcleo de
denota el núcleo de
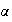 ).
).
Demostración. 1) Supóngase que
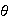 es un homomorfismo inyectivo y sea
es un homomorfismo inyectivo y sea
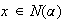 . Entonces
. Entonces
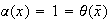 ;
;
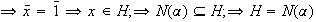 . Recíprocamente, sea
. Recíprocamente, sea
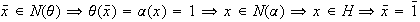 .
.
Puesto que
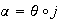 ,
entonces siendo
,
entonces siendo
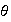 sobreyectivo,
sobreyectivo,
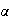 lo es ya que
lo es ya que
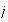 es el homomorfismo canónico.
es el homomorfismo canónico.
Supóngase ahora que
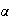 es sobreyectivo, y sea
es sobreyectivo, y sea
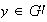 .
Entonces, existe
.
Entonces, existe
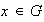 tal que
tal que
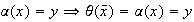 ,
es decir,
,
es decir,
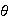 es sobreyectivo.
es sobreyectivo.
2) Es consecuencia directa del teorema.
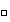
Las afirmaciones siguientes evidencian la aplicabilidad del teorema de factorización.
Corolario 3. Sea
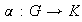 un homomorfismo sobreyectivo de grupos y sea
un homomorfismo sobreyectivo de grupos y sea
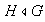 .
Entonces
.
Entonces
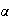 induce el homomorfismo sobreyectivo
induce el homomorfismo sobreyectivo
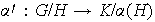
definido por
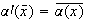 ,
donde
,
donde
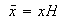 y
y
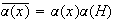 .
Además,
.
Además,
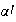 es inyectivo (y por lo tanto un isomorfismo) si y sólo si
es inyectivo (y por lo tanto un isomorfismo) si y sólo si
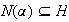 .
.
Corolario 4. Sea
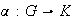 un homomorfismo de grupos y sea
un homomorfismo de grupos y sea
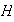 un subgrupo normal de
un subgrupo normal de
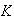 .
.
Entonces
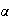 induce el homomorfismo inyectivo
induce el homomorfismo inyectivo
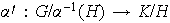
definido por
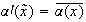 ,
,
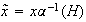 ,
,
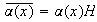 . Además, si
. Además, si
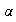 es sobreyectivo, entonces
es sobreyectivo, entonces
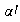 es un isomorfismo.
es un isomorfismo.
Corolario 5. Sea
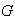 un grupo y sean
un grupo y sean
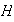 y
y
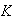 subgrupos normales de
subgrupos normales de
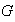 tales que
tales que
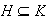 . Entonces se tiene el homomorfismo sobreyectivo
. Entonces se tiene el homomorfismo sobreyectivo

definido por
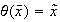 , donde
, donde
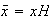 y
y
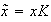 .
.