| Lección 1. |
Ciclos - Concepto
|
Definición 1. Sea
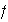 un elemento de
un elemento de
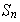 .
Se dice que f es un ciclo de longitud
.
Se dice que f es un ciclo de longitud
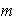 ,
,
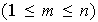 ,
si existen
,
si existen
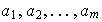 elementos diferentes de
elementos diferentes de
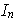 tales que
tales que
1)
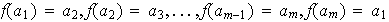 ,
,
2)
 para
para
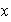
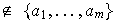 .
.
Se denota a
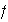 por
por
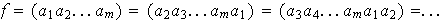
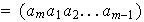
Nótese que un ciclo de longitud
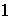 es la idéntica en
es la idéntica en
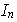 .
.
Sean
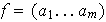 y
y
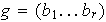 dos ciclos de
dos ciclos de
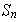 .
Se dice que
.
Se dice que
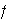 y
y
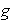 son dos ciclos disyuntos si
son dos ciclos disyuntos si
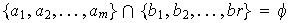
Nótese que las permutaciones
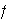 y
y
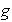 de
de
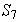 son ciclos disyuntos:
son ciclos disyuntos:
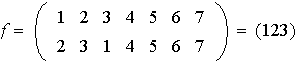
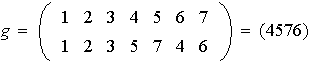
Proposición 1. En
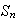 el producto de ciclos disjuntos conmuta.
el producto de ciclos disjuntos conmuta.
Demostración. Sean
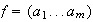 y
y
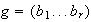 dos ciclos disyuntos de
dos ciclos disyuntos de
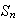 .
Sea
.
Sea
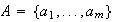 y
y
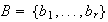 .
Sea
.
Sea
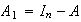 y
y
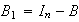 .
Dado
.
Dado
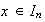 existen tres posibilidades
existen tres posibilidades
1)
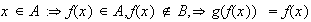 ;
;
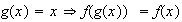
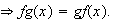
2)
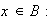 es análogo al anterior.
es análogo al anterior.
3)
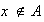 y
y
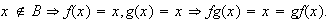
De 1), 2) y 3) se desprende que
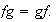
La importancia de la anterior proposición se pone de manifiesto en el siguiente teorema.
Teorema 1. 1) Sea
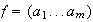 un ciclo de longitud m de
un ciclo de longitud m de
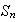 .
Entonces
.
Entonces
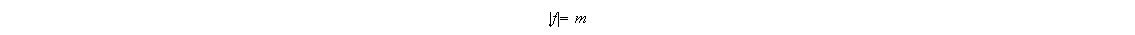
2) Sea
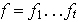 una
permutaci\on de
una
permutaci\on de
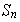 donde
donde
 son
ciclos disyuntos de longitudes
son
ciclos disyuntos de longitudes
 respectivamente.
Entonces
respectivamente.
Entonces
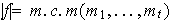
Demostración. 1) Probemos en primer lugar que
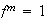 :
si
:
si
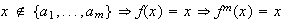 .
Sea
.
Sea
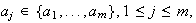
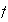 se puede expresar también como
se puede expresar también como
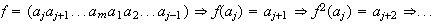
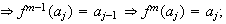 es decir,
es decir,
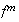 actua también como 1 sobre los elementos de
actua también como 1 sobre los elementos de
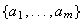 .
.
El orden de
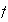 es el menor entero positivo
es el menor entero positivo
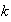 tal que
tal que
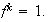 Supóngase que existe
Supóngase que existe
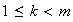 tal que
tal que
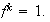
 ,
pero esto es una contradicción ya que los elementos del ciclo
,
pero esto es una contradicción ya que los elementos del ciclo
 son diferentes.
son diferentes.
Lo anterior prueba que
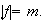
2) La demostración se efectua por inducción sobre
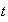 .
.
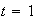 :
La afirmación es consecuencia de 1).
:
La afirmación es consecuencia de 1).
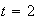 :
:
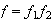 ,
donde
,
donde
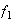 y
y
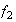 son ciclos disyuntos de longitudes
son ciclos disyuntos de longitudes
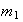 y
y
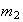 respectivamente. Según la Proposición 1,
respectivamente. Según la Proposición 1,
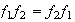 .
Además,
.
Además,
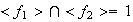 .
En efecto, sea
.
En efecto, sea
 tal que
tal que
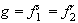 con
1
con
1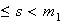 y
1
y
1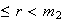 .
Sea
.
Sea
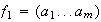 .
Puesto que
.
Puesto que
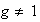 existe
existe
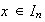 tal que
tal que
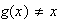 .
Necesariamente
.
Necesariamente
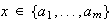 .
Sea pues
.
Sea pues
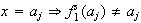 pero
pero
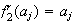 ,
contradicción.
,
contradicción.
Así pues,
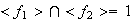 ,
,
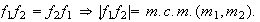
Supongamos que la afirmación es cierta para
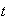 :
sea
:
sea
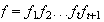 ,
donde
,
donde
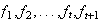 son ciclos disyuntos dos a dos y de longitudes
son ciclos disyuntos dos a dos y de longitudes
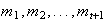 respectivamente. Sea
respectivamente. Sea
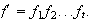 Entonces
Entonces
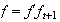 .
Nótese que
.
Nótese que
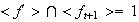 .
Además
.
Además
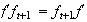 ;
entonces
;
entonces
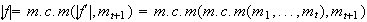
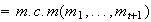 .
.