| Lección 2. |
Teorema
|
Teorema 2. Cada
permutación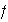 
de
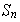es representable como producto de ciclos disyuntos dos a dos. Tal
representación es única salvo el orden y la inclusión de ciclos
de longitud
.
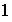Demostración. La existencia se realiza por induccion sobre n.
:
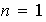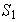sólo posee un elemento, el cual es un ciclo de longitud 1.
Supóngase que la afirmación es válida para toda
permutación de un conjunto de
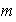elementos con
.
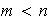Sea
.
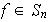Si
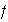es un ciclo entonces no hay nada que probar. Sea
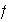una permutación que no es un ciclo. Esto en particular implica que
.
Existe entonces
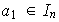tal que
.
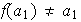Cosideramos la sucesión
.
En esta sucesión se tiene un número finito de elementos diferentes
de
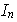debido a que para cada k
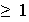
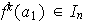y
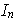es finito.
Por lo tanto existen
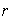y
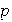enteros positivos diferentes (por ejemplo
)
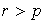tales que
.
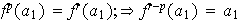Sea
.
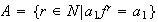Según lo dicho anteriormente,
.
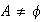Como
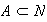y
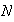es bien ordenado
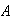posee entonces primer elemento
,
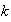es decir,
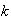es el menor entero positivo tal que
.
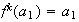Los elementos
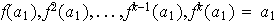
son diferentes, ya que en caso contrario exixtiría un
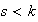talque
.
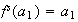La permutación
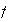determina así el
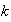-ciclo
,
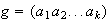donde
.
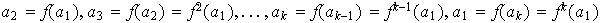Consideremos la permutación
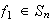definida por
,
,
,
.
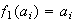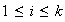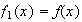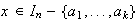Nótese que
.
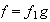En efecto, si
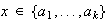entonces sea
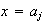para algún
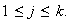Si
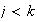entonces
.
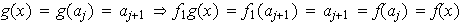Si
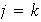entonces
.
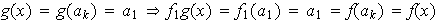Ahora si
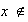
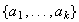entonces
.
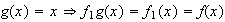Puesto que
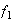fija los elementos
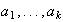entonces
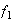puede considerarse como una permutación del conjunto
.
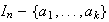Por la hipótesis de induccion
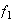es producto de ciclos disyuntos conformados por los elementos de
.
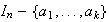En total
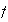es producto de ciclos disyuntos conformados por los elementos de
.
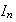Esto completa la prueba de la primera afirmación del teorema.
Probemos ahora la unicidad de la desconposición:
Sean
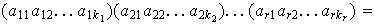
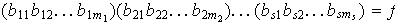dos
descomposiciones de
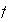en producto de ciclos disyuntos. Nótese que
.
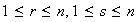Estamos considerando que los elementos de
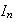que permanezcan fijos bajo
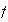conforman ciclos de longitud 1, es decir,
;
.
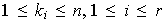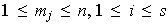En otras palabras estamos considerando que
.
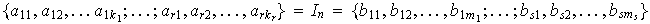El elemento
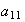debe aparecer en alguno de los ciclos de la segunda descomposición. Por
la conmutatividad de los factores podemos considerar que
.
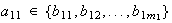Reordenando el ciclo
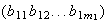podemos considerar sin perdida de generalidad que
.
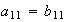Según el Teorema 1,
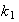es el menor entero positivo talque
.
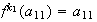Se obtiene pues que
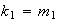y además
;
;
...;
;
,
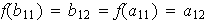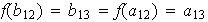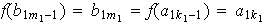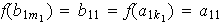es decir,
.
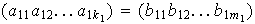El mismo análisis podemos aplicar a
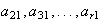demostrando que
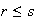y la igualdad de ciclos.
Similarmente
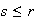lo cual concluye la prueba del teorema.
Ejemplo 1.
.
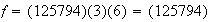
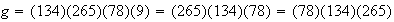
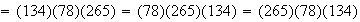