| Lección 3. |
El Grupo Alternante
|
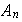
Definición 2. Para
,
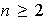los ciclos de longitud
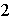de
se conocen como transposiciones .
Teorema 3. Cada permutación de
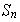es
representable como un producto finito de transposiciones.
Demostración. Puesto que cada permutacion es
representable como un producto de ciclos disyuntos entonces es suficiente
demostrar el teorema para cada ciclo. Sea
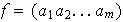un
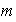-ciclo.
Si
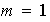entonces
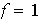y
.
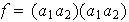Sea pues
.
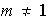Nótese que
.
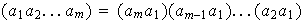Observación 1. 1) A diferencia del teorema de la lección anterior la representación de una permutación en producto de transposiciones no es única
.
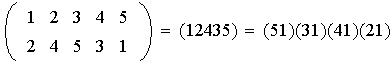
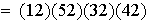2) Según el teorema anterior, cada permutación
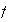de
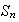es representable como un número finito
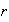de transposiciones; además se vió que dicha representación no
es única. De tal manera que padría presentarse la posibilidad de que
en una descomposición
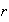sea par y en otra
sea impar. Sin embargo, la siguiente proposición muestra que tal
situación es imposible.
Proposición 2.
Sea
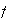una permutación de
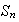la cual tiene dos descomposiciones en producto de
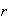y
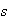transposiciones. Entonces,
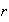es par si y sólo si
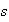es par.
Demostración. Sea
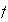una permutación de
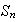para la cual tiene dos descomposiciones en producto de transposiciones
.
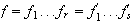
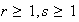Consideremos el natural
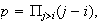
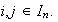(Por ejemplo para n=4 se tiene que
).
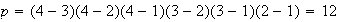Sea
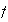una permutación cualquiera de
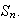Definamos la acción de
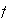sobre
como
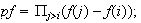
Nótese que
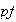es un entero (no necesariamente positivo como
);
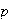los factores
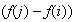que conforman
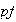son diferencias de elementos de
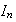y además
.
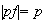En efecto, demostraremos que siendo
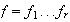, donde cada
,
,
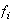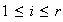es una transposición, entonces
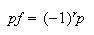
a) sea
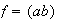una transposición con
.
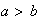Los factores
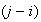de
en los cuales no intervienen 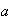ni
ni
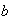no cambian al aplicar
.
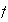Consideremos pues aquellos factores donde aparescacan
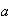o
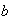o ambos. Se presentan entonces las siguientes posibilidades.
i) Factores donde aparece
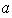pero no
:
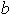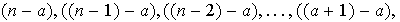
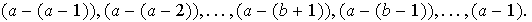
Al aplicar
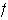a los factores de la primera fila obtenemos
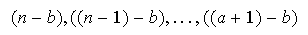y no hay cambios de signo.
Al aplicar
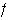a los factores de la seguda fila obtenemos
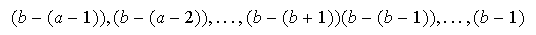y hay
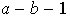cambios de signo.
ii) Los factores donde aparece
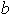pero no
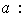
Aplicando
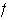a los factores anteriores obtenemos
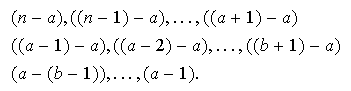
se presenta en este caso
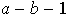cambios de signo.
iii) Factor donde aparece
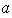y
:
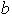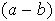
Al aplicar f obtenemos
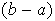y hay un cambio de signo.
En total al aplicar
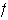a
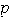se efectuan
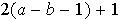cambios de signos y así
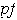tiene signo menos.
Nótese que los factores de i) mediante
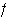se convierten en los factores de ii) con algunos signos cambiados, y a su vez
los de ii) en los de i) con algunos signos cambiados. De lo anterior se
desprende que
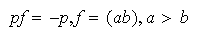
b) Siendo
un producto de
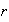transposiciones entonces
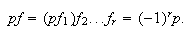
c)
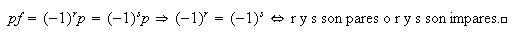
Según la proposición anterior se pueden distinguir aquellas permutaciones que son producto de un número par de transposiciones.
Teorema 4. Sea
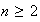y
es producto de un número par de
transposiciones
.
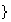Entonces,
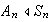y se denomina el grupo alternante o grupo de permutaciones pares. Además,
\
.
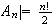Demostración. Claramente
.
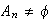Además, según la proposición anterior el producto de dos
permutaciones pares es par con lo cual
(
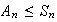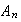es finito).
Probemos ahora que
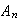es normal en
.
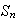Consideremos la función signo
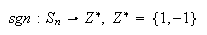
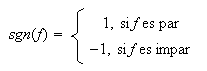
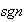es un homomorfismo: Sean
.
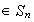Entonces se presentan las siguientes posibilidades:
y
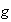pares: entonces
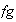es par y así
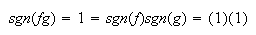
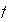es par y
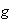es impar: entonces
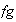es impar y así
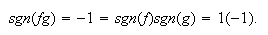
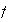es impar y
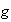es par: análogo al anterior.
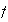y
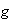impares: entonces fg es par y así
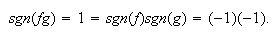
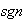es una función sobre:
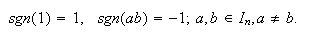
Según el teorema fundamental de homomorfismo
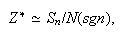
pero
,
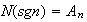así pues,
.
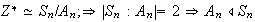Notese además que
.