| Lección 4. |
Sistemas de Generadores
|
Ya hemos visto que el subconjunto de todos los ciclos como también el
conjunto de todas las transposiciones constituyen sistemas de generadores para
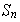 .
.
Queremos en esta lección mostrar otros sistemas más reducidos de generadores.
Proposición 3. 1)
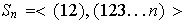
2)
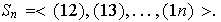
Demostración. Es suficiente demostrar 1) ya que
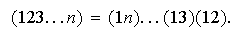
Sea
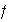 una permutación de
una permutación de
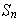 .
Entonces
.
Entonces
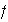 es producto de ciclos disyuntos; basta pues probar que cada ciclo está en
el generado por
es producto de ciclos disyuntos; basta pues probar que cada ciclo está en
el generado por
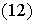 y
y
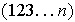 .
Sea
.
Sea
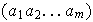 un
un
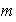 -ciclo
de
-ciclo
de
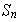 .
Entonces
.
Entonces
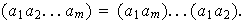 Nótese que cada transposición
Nótese que cada transposición
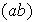 se puede escribir como
se puede escribir como
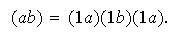
Probemos entonces que cada transposición de la forma
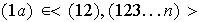
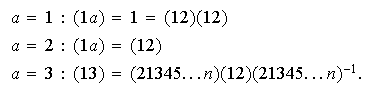
Pero nótese que
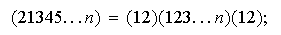 por tanto
por tanto
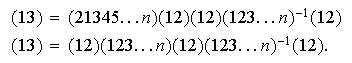
En general
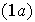 ,
con
,
con
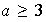 ,
se puede expresar como
,
se puede expresar como
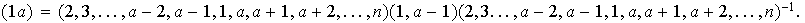
Suponiendo inductivamente que
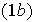 está en el subgrupo generado por
está en el subgrupo generado por
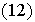 y
y
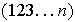 ,
siendo
,
siendo
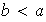 ,
entonces resta probar que
,
entonces resta probar que
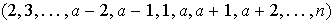 está en el mencionado subgrupo.
está en el mencionado subgrupo.
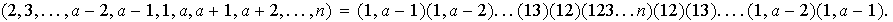
Según la hipotesis inductiva
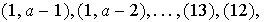 están en
están en
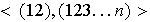 .
Esto completa la demostración de la proposición.\
.
Esto completa la demostración de la proposición.\
Proposición 4. Para
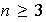 ,
,
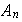 coincide con con el subgrupo generado por los
coincide con con el subgrupo generado por los
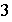 -ciclos.
-ciclos.
Demostración. Sea
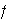 una permutación par. Podemos agrupar las transposiciones de
una permutación par. Podemos agrupar las transposiciones de
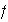 de dos en dos y probar que cada pareja así constituida es producto de
de dos en dos y probar que cada pareja así constituida es producto de
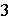 -ciclos.
-ciclos.
Sean pues
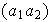 y
y
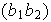 dos transposiciones cualesquiera. Consideremos dos casos posibles
dos transposiciones cualesquiera. Consideremos dos casos posibles
1)
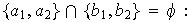
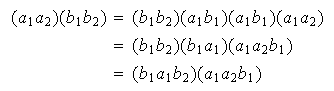 ya que
ya que
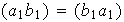 .
.
2)
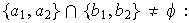
Si
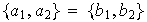 entonces
entonces
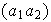 =
=
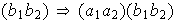
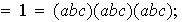 hemos utilizado el hecho de que
hemos utilizado el hecho de que
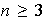 .
.
Si
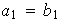 pero
pero
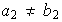 entonces
entonces
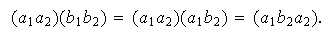
Si
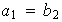 pero
pero
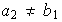 entonces se obtiene un 3-ciclo como en el caso anterior.\
entonces se obtiene un 3-ciclo como en el caso anterior.\
Proposición 5 (Teorema de Jordan). Sea
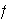 una permutación cuaquiera de
una permutación cuaquiera de
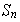 .
Entonces para cada ciclo
.
Entonces para cada ciclo
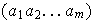 se
tiene que
se
tiene que

Demostración. Puesto que cada permutación es
producto de transposiciones es entonces suficiente suponer que
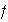 es una pernutación
es una pernutación
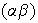 .
Consideremos dos casos posibles
.
Consideremos dos casos posibles
1)
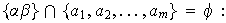
 ya que
ya que
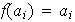 para
para

2)
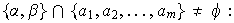 se presentan entonces dos situaciones:
se presentan entonces dos situaciones:
a)
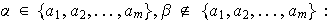 sea
sea
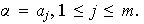 Entonces
Entonces
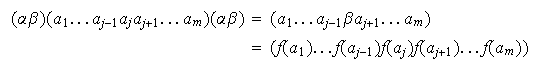
b)
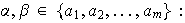 Sea
Sea
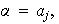
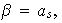
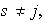
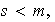
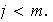 Entonces
Entonces

Por último, si por ejemplo
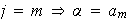 y entonces
y entonces