| Lección 5. |
El Grupo Dihédrico
 ,
|
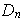Consideremos un polígono regular de
lados. Como ilustración consideremos un un pentágono y un
hexágono:
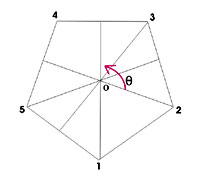
Por simetrías de un polígono regular de
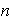lados se entienden el siguiente conjunto de movimientos de dicho
polígono.
1)
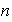rotaciones en sentido contrario al movimiento de las manecillas del reloj a
través de los ángulos
,
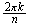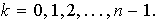
2)
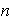reflexiones correspondientes a los
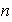ejes de simetría.
Para el caso en que
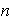sea par los ejes de simetría son: a)
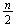líneas obtenidas uniendo el centro
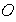del polígono con cada uno de sus vértices 1,2,...,n.
b)
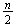líneas obtenidas uniendo el centro
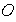con los puntos medios de los
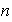lados del polígono.
Para el caso en que
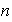es impar las
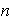reflexiones corresponden a los
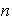ejes de simetría obtenidos uniendo el centro
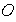del polígono con sus
.
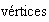Este conjunto de
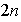movinientos constituye un grupo bajo la operación de composición de
movimientos, y se denomina el grupo dihédrico de grado
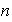, y se denota por
.
El grupo dihédrico
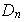como subgrupo de
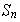: sea
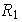la rotación a través del ángulo
.
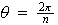Esta rotación corresponde a la permutación de los
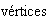dada por
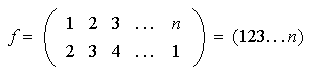
Si denotamos la rotación a través del ángulo
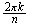por
,
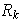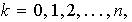entonces a
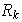corresponde
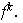Nótese que
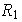es un elemento de
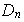de orden
:
,
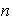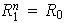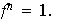
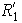es la reflexión a través del eje de simetría que pasa por el
vértice 1. Esta reflexión corresponde a la permutación de los
vértices dada por
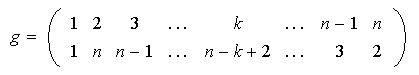
Nótese que
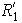tiene orden 2:
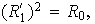
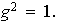Por último nótese que
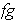es de orden
,
de donde
,
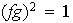luego
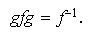
Generadores y relaciones generadoras del grupo dihédrico
: consideremos la rotación y reflexión anteriores las cuales podemos
identificar con las permutaciones
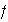y
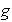, respectivamente. Desde luego que
.
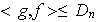Si probamos que
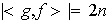entonces tendríamos que
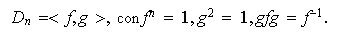
Sea
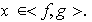Entonces
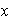tiene la forma
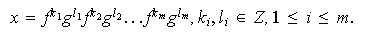
Puesto que
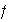es un elemento de orden
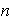y
un elemento de orden
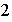podemos considerar que
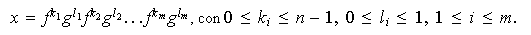
Considérese el producto
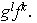Si
,
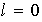entonces
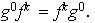Sea pues
.
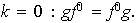
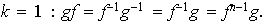
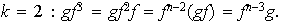
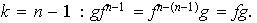
De lo anterior se concluye que cada elemento
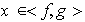tiene la forma
,
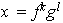con
,
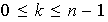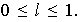Resultan
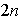elementos . Comprobemos que ellos son diferentes. Sea
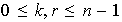y
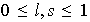tales que
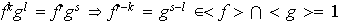(de lo contrari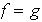o
ó
,
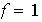lo cual es
falso)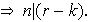
Siendo
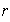y
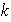con las condiciones dadas sólo puede tenerse que
.
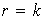Análogamente
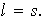
De lo anterior obtenemos que
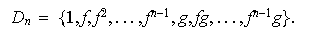
Sea
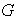un grupo generado por los elementos
y
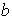tales que
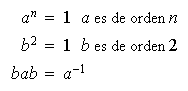
Entonces es posible repetir la prueba realizada anteriormente para comprobar
que
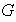tiene
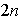elementos diferentes a
saber
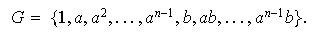
La función
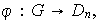definida por
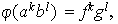
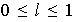define un isomorfismo.
Representación matricial del grupo dihédrico:
consideremos en
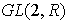las matrices
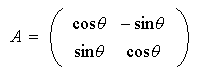
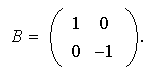
con
.
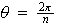Nótese que
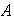es de orden
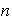y
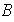es de orden
.
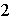Además
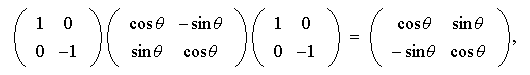
es decir
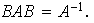Esto indica que
es isomorfo al grupo dihédrico. La matriz
representa la rotación del sistema de coordenadas
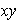a través de de un ángulo
;
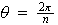la matriz B representa una reflexión de dicho sistema .
Nótese que en
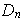se tiene entonces la siguiente regla de multiplicación:
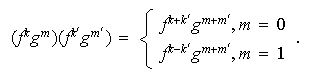
Algunos subgrupos de
.
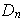Por los generadores de
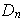podemos presentar inmediatamente los siguientes subgrupos:
De orden
:
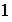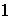
De orde
:
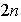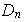
De orden
:
.
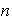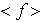Como se observó, en
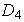este no es el único subgrupo de orden
.
Puesto que
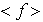es cíclico entonces por cada divisor de
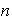tendremos al menos un subgrupo de orden
.
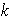Los subgrupos de orden
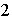son:
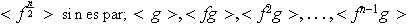
Centro de
.
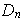Para todo
,
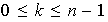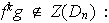en efecto,
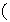
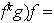
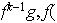
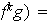
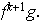Si fuese
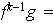
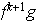entonces
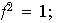pero
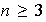y
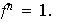
De lo anterior obtenemos que
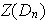contiene solamente rotaciones: Sea
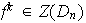con
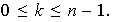Entonces
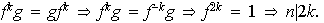
Cuando
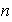es impar
Sea
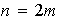par. Como
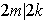entonces existe
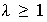tal que
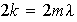
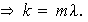Si fuese
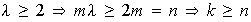contradicción; por lo tanto
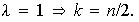
De lo anterior obtenemos que si
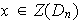entonces
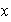es de la forma
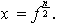Veamos que realmente en este caso
par
:
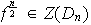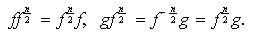
Obtenemos que
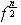conmuta con cada elemento de
,
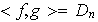es decir,
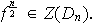
De lo dicho obtenemos que
