| Lección 6. |
Subgrupos Normales del Grupo
 , ,
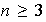
|
Sea
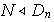 .
Consideremos los siguientes casos posibles:
.
Consideremos los siguientes casos posibles:
1)
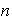 es impar y
es impar y
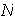 no contiene reflexiones: en este caso
no contiene reflexiones: en este caso
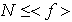 y existe entonces un divisor positivo
y existe entonces un divisor positivo
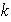 de
de
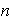 tal que
tal que
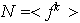 .
Veamos que cada subgrupo de este tipo es efectivamente normal en
.
Veamos que cada subgrupo de este tipo es efectivamente normal en
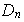 :
:
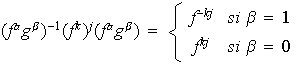
2)
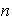 es impar y en
es impar y en
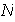 hay al menos una reflexión: sea
hay al menos una reflexión: sea
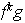 en
en
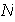 ,
donde
,
donde
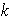 es fijo y cumple
es fijo y cumple
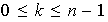 .
Sea
.
Sea
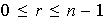 ,
entonces
,
entonces
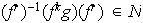 ,
luego
,
luego
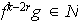 .
Tomando
.
Tomando
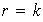 se tiene que
se tiene que
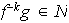 y entonces
y entonces
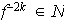 .
Tomemos ahora
.
Tomemos ahora
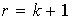 ,
entonces
,
entonces
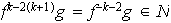 y entonces
y entonces
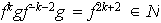 .
De aquí resulta entonces que
.
De aquí resulta entonces que
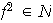 .
Como
.
Como
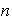 es impar,
es impar,
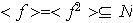 ,
es decir,
,
es decir,
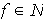 .
Finalmente,
.
Finalmente,
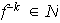 y entonces
y entonces
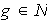 .
Esto garantiza que
.
Esto garantiza que
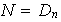 .
.
3)
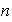 es par y
es par y
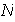 no contiene reflexiones: razonando como en el caso impar se obtiene que existe
entonces un divisor positivo
no contiene reflexiones: razonando como en el caso impar se obtiene que existe
entonces un divisor positivo
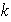 de
de
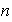 tal que
tal que
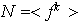 .
.
4)
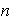 es par y en
es par y en
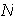 hay al menos una reflexión: sea
hay al menos una reflexión: sea
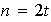 y sea
y sea
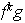 en
en
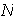 ,
donde
,
donde
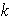 es fijo y cumple
es fijo y cumple
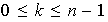 .
Al igual que en el caso impar podemos concluir que
.
Al igual que en el caso impar podemos concluir que
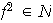 .
Consideremos dos casos posibles:
.
Consideremos dos casos posibles:
a)
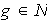 :
entonces el siguiente conjunto de
:
entonces el siguiente conjunto de
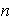 elementos distintos está incluido en
elementos distintos está incluido en
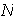 :
:
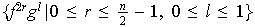 .
Si
.
Si
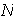 posee al menos un elemento adicional, entonces
posee al menos un elemento adicional, entonces
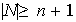 y esto implica que
y esto implica que
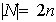 .
En efecto,
.
En efecto,
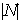 divide a
divide a
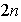 y entonces
y entonces
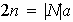 ;
si
;
si
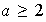 entonces
entonces
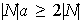 ,
luego
,
luego
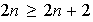 , lo cual es falso. Así pues, si
, lo cual es falso. Así pues, si
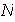 no posee al menos un elemento adicional, entonces
no posee al menos un elemento adicional, entonces
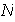 es exactamente el subgrupo
es exactamente el subgrupo
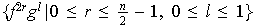 .
En caso contrario,
.
En caso contrario,
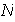 coincide con
coincide con
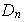 .
.
b)
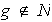 :
veamos que entonces necesariamente
:
veamos que entonces necesariamente
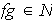 .
En efecto,
.
En efecto,
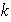 debe ser impar, ya que de lo contrario
debe ser impar, ya que de lo contrario
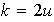 y entonces
y entonces
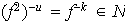 ,
con lo cual
,
con lo cual
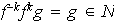 ,
lo cual es falso. Así pues,
,
lo cual es falso. Así pues,
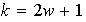 y esto implica que
y esto implica que
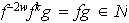 .
.
Nótese que entonces
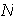 contiene al conjunto
contiene al conjunto
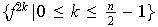 y también al conjunto
y también al conjunto
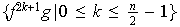 ,
la reunión de los cuales tiene
,
la reunión de los cuales tiene
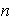 elementos. Como se vió anteriormente, si
elementos. Como se vió anteriormente, si
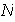 posee al menos un elemento adicional, entonces
posee al menos un elemento adicional, entonces
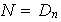 ,
en caso contrario
,
en caso contrario
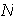 es exactamente la reunión de estos dos conjuntos.
es exactamente la reunión de estos dos conjuntos.
En conclusión, los subgrupos normales de
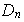 se caracterizan de la siguiente manera:
se caracterizan de la siguiente manera: