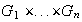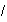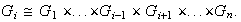SEDE BOGOTA

Productos y Sumas Directas

Lección 1.

Producto Cartesiano: Caso Finitos

Sea una colección finita de grupos (tomados con notación multiplicativa) y sea

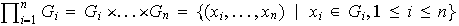
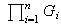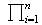
el producto cartesiano conjuntista de la familia dada. Se pretende definir en una operación binaria bajo la cual 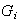$\ \prod_{i=1}^{n}$ $G_{i}$ tenga estructura de grupo.

Definición 1. Sea 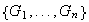una familia finita de grupos (multiplicativos) y sea 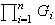el producto cartesiano de los conjuntos 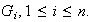El producto de 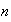-plas definido por

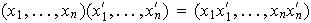
da a 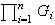una estructura de grupo. La pareja 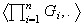así constituida se denomina producto cartesiano de la familia

En efecto....

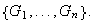
Observación 1. Si los grupos 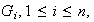presentan notación aditiva entonces la operación entre 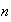-plas se denota por

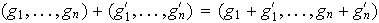
En este caso el neutro y los opuestos toman la forma

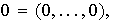
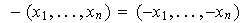
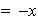
Ejemplo 1. 1) Sea 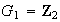y 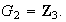Entonces los elementos de 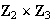son

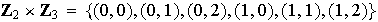
Nótese que 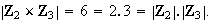Más aún, 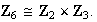¿Quiere ver porqué ?

2) Sea 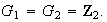Entonces los elementos de son

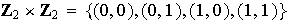
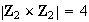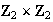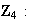
Obsérvese que pero no es isomorfo a $\QTR{bf}{Z}_{4}:$

no es cíclico, no es isomorfo con

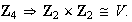
Algunas propiedades del producto cartesiano se presentan en las siguientes proposiciones.

Proposición 1. Sea 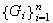una familia de grupos cualesquiera. Entonces:

1) $G_{2}\times G_{1}.$

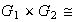
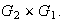
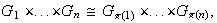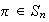
2) para cada $\pi\in S_{n}$

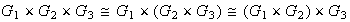
4) El producto cartesiano tiene la propiedad asociativa generalizada.

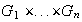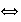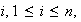
5) es abeliano para cada 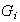$i,1\leq i\leq n,$ $G_{i}$ es abeliano.

Proposición 2. 1) Sea 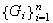una familia de grupos finitos. Entonces:

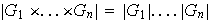
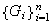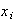2) Sea una familia finita de grupos cualesquiera y sea tal que $x_{i}$ es de orden finito para cada

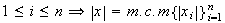
3) Si 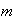y 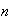son enteros positivos primos relativos, entonces

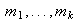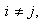
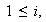
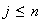4) Sean $\ m_{1},...,m_{k}$ enteros positivos tales que $(m_{i},m_{j})=1$ para $\ i\neq j,$ $\ 1\leq i,$ $\ j\leq n$ . Entonces

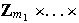
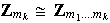
5) Sea 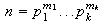la descomposición del entero 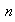$\ n$ en factores primos. Entonces

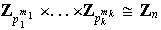
Proposición 3. Sea 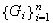una familia finita de grupos. Entonces

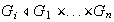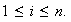
1) para cada $1\leq i\leq n.$