| Lección 2. |
Producto Cartesiano: Caso Infinito
|
Sea
 una familia cualquiera de grupos. Sea
una familia cualquiera de grupos. Sea
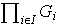 el producto cartesiano de los conjuntos de la familia dada, es decir,
el producto cartesiano de los conjuntos de la familia dada, es decir,

Definimos en
 el producto de manera análoga a como se hizo en el caso finito.
Escribiendo
el producto de manera análoga a como se hizo en el caso finito.
Escribiendo
 y
y
 como
como
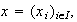 entonces
entonces

Nótese que este producto da a
 una estructura de grupo, cuyo elemento neutro es
una estructura de grupo, cuyo elemento neutro es
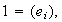 donde
donde
 para cada
para cada

El inverso de

 es entonces
es entonces

Cuando
 entonces el producto
entonces el producto
 coincide logicamente con la definición de producto cartesiano dada en la
lección anterior.
coincide logicamente con la definición de producto cartesiano dada en la
lección anterior.
Las proyecciones canónicas se definen por:




El producto cartesiano junto con sus proyecciones están caracterizadas por la siguiente propiedad universal:
Teorema 1. Sea
 una familia de grupos de naturaleza arbitraria, sea
una familia de grupos de naturaleza arbitraria, sea
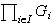 su producto cartesiano y sean
su producto cartesiano y sean


 las proyecciones canónicas. Entonces
las proyecciones canónicas. Entonces
1) Para cada grupo
 con homomorfismos
con homomorfismos


 existe un único homomorfismo
existe un único homomorfismo
 de
de
 en
en
 tal que para cada
tal que para cada
 el siguiente diagrama es conmutativo:
el siguiente diagrama es conmutativo:

2) Cualquier otro grupo
 con homomorfismos
con homomorfismos
 que tenga la propiedad 1) es isomorfo al producto cartesiano.
que tenga la propiedad 1) es isomorfo al producto cartesiano.
Demostración. 1) Por la forma
como fue definido
 y la manera como se operan los elementos del producto cartesiano se ve
claramente que
y la manera como se operan los elementos del producto cartesiano se ve
claramente que
 es un homomorfismo de grupos que hace conmutativo el diagrama para cada
es un homomorfismo de grupos que hace conmutativo el diagrama para cada

Sea
 otro homomorfismo de
otro homomorfismo de
 en el producto que hace conmutativos los diagramas; sea
en el producto que hace conmutativos los diagramas; sea
 .
Entonces,
.
Entonces,
 para cada
para cada

2) Puesto que tanto
 como el producto tienen la propiedad 1) entonces para cada
como el producto tienen la propiedad 1) entonces para cada
 los siguientes diagramas conmutan
los siguientes diagramas conmutan
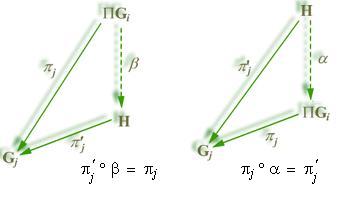
De lo anterior obtenemos:



Considerando nuevamente que
 y el producto tienen la propiedad universal
y el producto tienen la propiedad universal

En vista de la unicidad,
 y
y
 Esto muestra que
Esto muestra que
 y
y
 son
isomorfos.
son
isomorfos.