| Lección 3. |
Suma Directa Externa
|
Sea
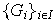 una familia de grupos y sea
una familia de grupos y sea
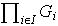 su grupo producto. Se denomina soporte de
su grupo producto. Se denomina soporte de
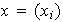 al subconjunto
al subconjunto
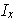 de
de
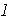 de elementos
de elementos
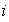 tales que
tales que
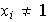 .
Definimos el conjunto
.
Definimos el conjunto
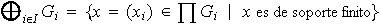 .
.
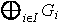 es un subgrupo del producto y se denomina suma directa
externa de la familia dada. En efecto,
es un subgrupo del producto y se denomina suma directa
externa de la familia dada. En efecto,
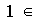
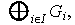 con lo cual la suma directa externa no es vacía. Sean
con lo cual la suma directa externa no es vacía. Sean
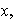
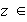
 con soportes
con soportes
 Entonces,
Entonces,
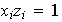 para cada
para cada
 Esto indica que sólo para los elementos de un cierto subconjunto finito
Esto indica que sólo para los elementos de un cierto subconjunto finito
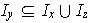 se
tiene que
se
tiene que
 Por lo tanto, si
Por lo tanto, si
 es el producto de
es el producto de
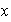 y
y
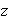 entonces
entonces
 Es claro que si
Es claro que si
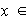
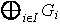 entonces
entonces
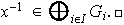
Asociadas a la suma directa externa de una familia de grupos están las siguientes inyecciones canónicas:
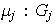
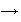
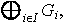
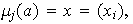 donde
donde
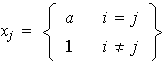
Evidentemente estas funciones son homomorfismos inyectivos.
Al igual que el producto, la suma directa externa con sus inyecciones canónicas está caracterizada por una propiedad universal.
Teorema 2.
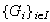 una familia de grupos de naturaleza arbitraria, sea
una familia de grupos de naturaleza arbitraria, sea
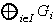 su suma directa externa y sean
su suma directa externa y sean
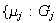
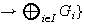 sus inyecciones canónicas. Entonces:
sus inyecciones canónicas. Entonces:
1) Para cada grupo
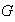 con homomorfismos
con homomorfismos
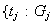
 existe un único homomorfismo
existe un único homomorfismo
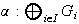
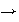
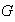 tal que para cada
tal que para cada
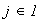 el siguiente diagrama es conmutativo
el siguiente diagrama es conmutativo
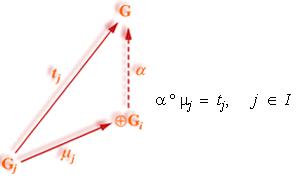
2) Cualquier otro grupo
 con homomorfismos
con homomorfismos
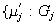
 que tenga la propiedad 1) es isomorfo a la suma directa externa.
que tenga la propiedad 1) es isomorfo a la suma directa externa.
Demostración. 1) Definimos
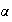 por
por

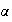 es un homomorfismo: si
es un homomorfismo: si
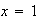 o
o
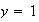 entonces evidentemente
entonces evidentemente
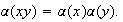 Supóngase pues que
Supóngase pues que
 y
y
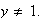 Sea
Sea
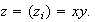 Si
Si
 entonces
entonces
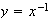 y asi
y asi
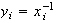 para cada
para cada
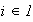 con lo cual
con lo cual
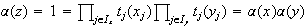
Sea entonces
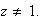 Se tiene que
Se tiene que
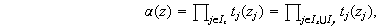 ya que
ya que
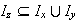
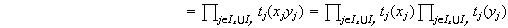
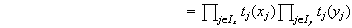

Probemos ahora la unicidad de
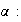 sea
sea
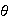 otro homomorfismo de
otro homomorfismo de
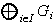 en
en
 tal que
tal que
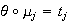 para cada
para cada
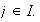 Sea
Sea
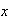 un elemento cualquiera de
un elemento cualquiera de
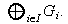 Si
Si
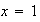 entonces necesariamente
entonces necesariamente
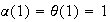 .
Considérese pues que
.
Considérese pues que
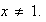 Entonces
Entonces
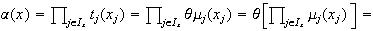
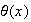 ya que
ya que
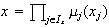
2) Por las propiedades de
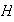 y
y
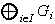 se tiene que para cada
se tiene que para cada
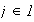 los siguientes diagramas conmutan:
los siguientes diagramas conmutan:
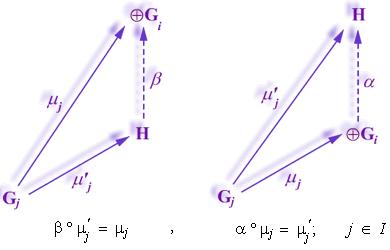
De lo anterior se desprende que
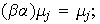
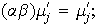

Como en el caso del producto cartesiano, de la unicidad se desprende que
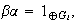
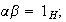 es decir,
es decir,
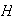 y
y
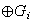 son grupos
isomorfos.
son grupos
isomorfos.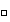
Observación 2. Nótese que cuando
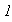
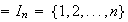 es un conjunto finito, entonces el producto cartesiano
es un conjunto finito, entonces el producto cartesiano
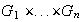 y la suma directa externa
y la suma directa externa
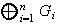 coinciden.
coinciden.